Question Number 138302 by mathdave last updated on 12/Apr/21
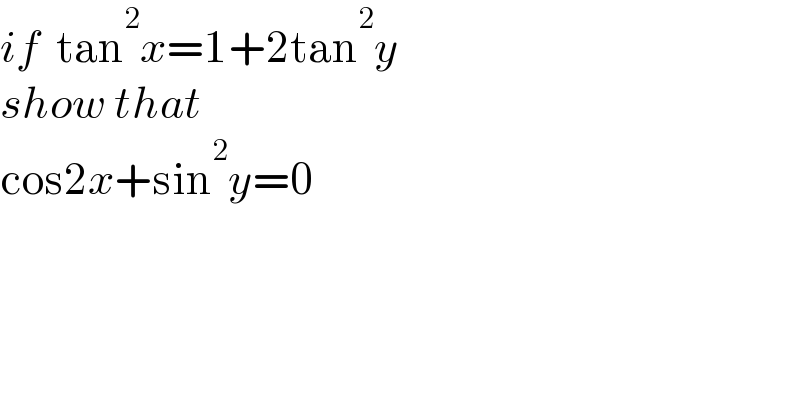
$${if}\:\:\mathrm{tan}^{\mathrm{2}} {x}=\mathrm{1}+\mathrm{2tan}^{\mathrm{2}} {y} \\ $$$${show}\:{that} \\ $$$$\mathrm{cos2}{x}+\mathrm{sin}^{\mathrm{2}} {y}=\mathrm{0} \\ $$
Answered by Ñï= last updated on 12/Apr/21

$$\mathrm{tan}\:^{\mathrm{2}} {x}=\mathrm{1}+\mathrm{2tan}\:^{\mathrm{2}} {y} \\ $$$$\Rightarrow\mathrm{sec}\:^{\mathrm{2}} {x}−\mathrm{1}=\mathrm{2sec}\:^{\mathrm{2}} {y}−\mathrm{1}\:\:\:\:\: \\ $$$$\Rightarrow\frac{\mathrm{2}}{\mathrm{cos}\:^{\mathrm{2}} {y}}=\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} {x}} \\ $$$$\Rightarrow\mathrm{2cos}\:^{\mathrm{2}} {x}=\mathrm{cos}\:^{\mathrm{2}} {y} \\ $$$$\Rightarrow\mathrm{cos}\:\mathrm{2}{x}+\mathrm{sin}\:^{\mathrm{2}} {y}=\mathrm{0} \\ $$
Answered by Ankushkumarparcha last updated on 12/Apr/21
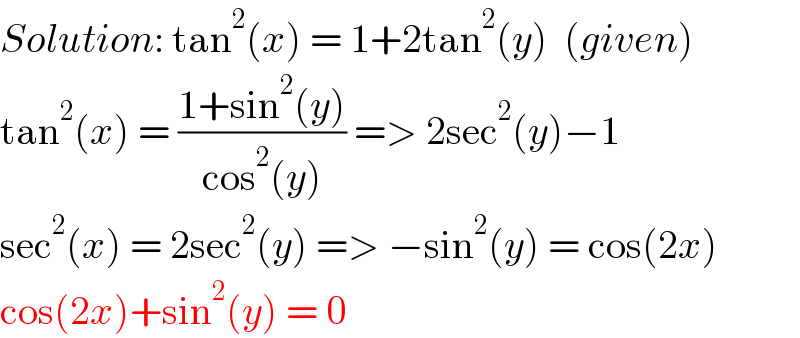
$${Solution}:\:\mathrm{tan}^{\mathrm{2}} \left({x}\right)\:=\:\mathrm{1}+\mathrm{2tan}^{\mathrm{2}} \left({y}\right)\:\:\left({given}\right) \\ $$$$\mathrm{tan}^{\mathrm{2}} \left({x}\right)\:=\:\frac{\mathrm{1}+\mathrm{sin}^{\mathrm{2}} \left({y}\right)}{\mathrm{cos}^{\mathrm{2}} \left({y}\right)}\:=>\:\mathrm{2sec}^{\mathrm{2}} \left({y}\right)−\mathrm{1} \\ $$$$\mathrm{sec}^{\mathrm{2}} \left({x}\right)\:=\:\mathrm{2sec}^{\mathrm{2}} \left({y}\right)\:=>\:−\mathrm{sin}^{\mathrm{2}} \left({y}\right)\:=\:\mathrm{cos}\left(\mathrm{2}{x}\right) \\ $$$$\mathrm{cos}\left(\mathrm{2}{x}\right)+\mathrm{sin}^{\mathrm{2}} \left({y}\right)\:=\:\mathrm{0} \\ $$
