Menu Close

If-tan2x-sin2x-b-and-tan2x-sin2x-a-prove-that-b-2-a-2-16ba-

Tinku Tara 0 Comments
Pin




Question Number 6655 by Tawakalitu. last updated on 09/Jul/16
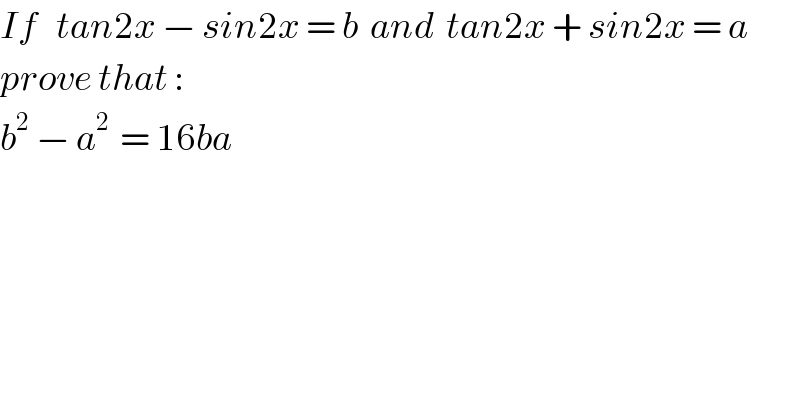
If tan2x − sin2x = b and tan2x + sin2x = a prove that : b^2 − a^(2 ) = 16ba
$${If}\:\:\:{tan}\mathrm{2}{x}\:−\:{sin}\mathrm{2}{x}\:=\:{b}\:\:{and}\:\:{tan}\mathrm{2}{x}\:+\:{sin}\mathrm{2}{x}\:=\:{a} \\ $$$${prove}\:{that}\::\: \\ $$$${b}^{\mathrm{2}} \:−\:{a}^{\mathrm{2}\:} \:=\:\mathrm{16}{ba} \\ $$
Commented by Yozzii last updated on 09/Jul/16
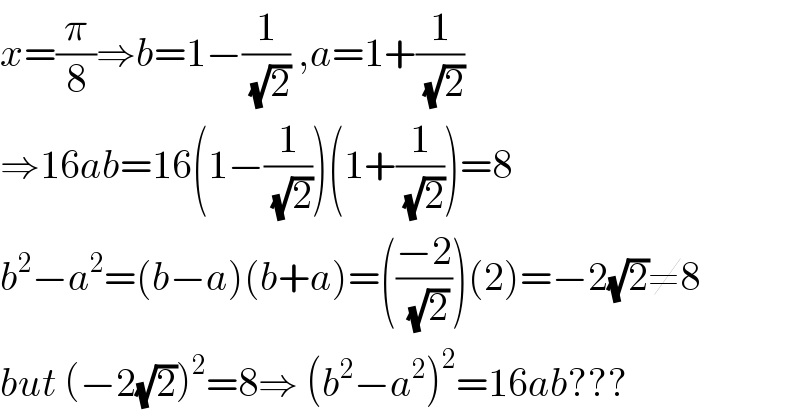
x=(π/8)⇒b=1−(1/( (√2))) ,a=1+(1/( (√2))) ⇒16ab=16(1−(1/( (√2))))(1+(1/( (√2))))=8 b^2 −a^2 =(b−a)(b+a)=(((−2)/( (√2))))(2)=−2(√2)≠8 but (−2(√2))^2 =8⇒ (b^2 −a^2 )^2 =16ab???
$${x}=\frac{\pi}{\mathrm{8}}\Rightarrow{b}=\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:,{a}=\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$\Rightarrow\mathrm{16}{ab}=\mathrm{16}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\left(\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)=\mathrm{8} \\ $$$${b}^{\mathrm{2}} −{a}^{\mathrm{2}} =\left({b}−{a}\right)\left({b}+{a}\right)=\left(\frac{−\mathrm{2}}{\:\sqrt{\mathrm{2}}}\right)\left(\mathrm{2}\right)=−\mathrm{2}\sqrt{\mathrm{2}}\neq\mathrm{8} \\ $$$${but}\:\left(−\mathrm{2}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} =\mathrm{8}\Rightarrow\:\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{16}{ab}??? \\ $$
Answered by Yozzii last updated on 09/Jul/16
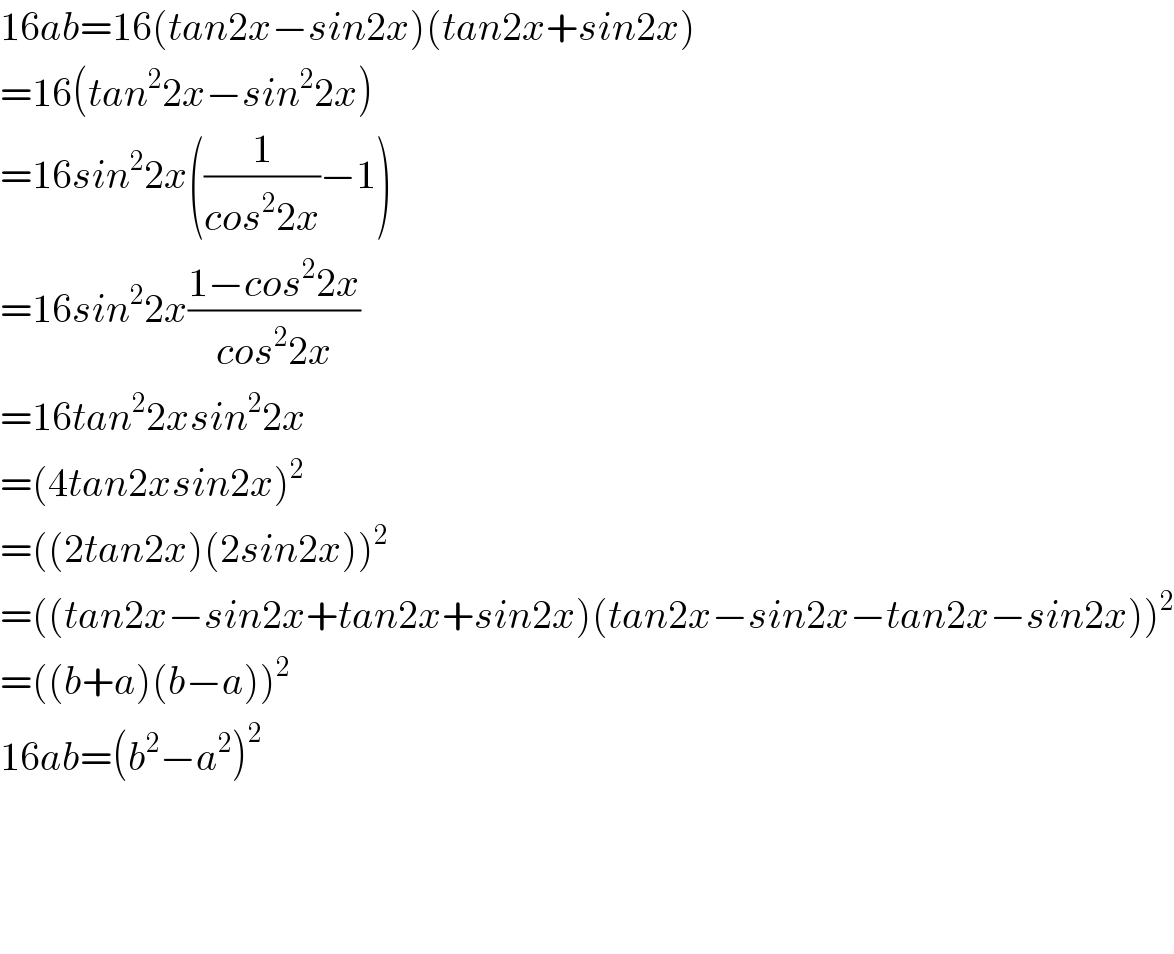
16ab=16(tan2x−sin2x)(tan2x+sin2x) =16(tan^2 2x−sin^2 2x) =16sin^2 2x((1/(cos^2 2x))−1) =16sin^2 2x((1−cos^2 2x)/(cos^2 2x)) =16tan^2 2xsin^2 2x =(4tan2xsin2x)^2 =((2tan2x)(2sin2x))^2 =((tan2x−sin2x+tan2x+sin2x)(tan2x−sin2x−tan2x−sin2x))^2 =((b+a)(b−a))^2 16ab=(b^2 −a^2 )^2
$$\mathrm{16}{ab}=\mathrm{16}\left({tan}\mathrm{2}{x}−{sin}\mathrm{2}{x}\right)\left({tan}\mathrm{2}{x}+{sin}\mathrm{2}{x}\right) \\ $$$$=\mathrm{16}\left({tan}^{\mathrm{2}} \mathrm{2}{x}−{sin}^{\mathrm{2}} \mathrm{2}{x}\right) \\ $$$$=\mathrm{16}{sin}^{\mathrm{2}} \mathrm{2}{x}\left(\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \mathrm{2}{x}}−\mathrm{1}\right) \\ $$$$=\mathrm{16}{sin}^{\mathrm{2}} \mathrm{2}{x}\frac{\mathrm{1}−{cos}^{\mathrm{2}} \mathrm{2}{x}}{{cos}^{\mathrm{2}} \mathrm{2}{x}} \\ $$$$=\mathrm{16}{tan}^{\mathrm{2}} \mathrm{2}{xsin}^{\mathrm{2}} \mathrm{2}{x} \\ $$$$=\left(\mathrm{4}{tan}\mathrm{2}{xsin}\mathrm{2}{x}\right)^{\mathrm{2}} \\ $$$$=\left(\left(\mathrm{2}{tan}\mathrm{2}{x}\right)\left(\mathrm{2}{sin}\mathrm{2}{x}\right)\right)^{\mathrm{2}} \\ $$$$=\left(\left({tan}\mathrm{2}{x}−{sin}\mathrm{2}{x}+{tan}\mathrm{2}{x}+{sin}\mathrm{2}{x}\right)\left({tan}\mathrm{2}{x}−{sin}\mathrm{2}{x}−{tan}\mathrm{2}{x}−{sin}\mathrm{2}{x}\right)\right)^{\mathrm{2}} \\ $$$$=\left(\left({b}+{a}\right)\left({b}−{a}\right)\right)^{\mathrm{2}} \\ $$$$\mathrm{16}{ab}=\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawakalitu. last updated on 09/Jul/16
Thanks so much
$${Thanks}\:{so}\:{much} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *