Menu Close

if-the-equations-of-the-sides-of-the-triangle-are-7x-y-10-0-x-2y-5-0-and-x-y-2-0-find-the-orhocentre-of-the-triangle-

Tinku Tara 0 Comments
Pin




Question Number 808 by sai dinesh last updated on 16/Mar/15
if the equations of the sides of the triangle are 7x+y−10=0,x−2y+5=0 and x+y+2=0, find the orhocentre of the triangle
$${if}\:{the}\:{equations}\:{of}\:{the}\:{sides}\:{of}\:{the}\:{triangle}\:{are}\:\mathrm{7}{x}+{y}−\mathrm{10}=\mathrm{0},{x}−\mathrm{2}{y}+\mathrm{5}=\mathrm{0}\:{and}\:{x}+{y}+\mathrm{2}=\mathrm{0},\:{find}\:{the}\:{orhocentre}\:{of}\:{the}\:{triangle} \\ $$
Commented by prakash jain last updated on 16/Mar/15
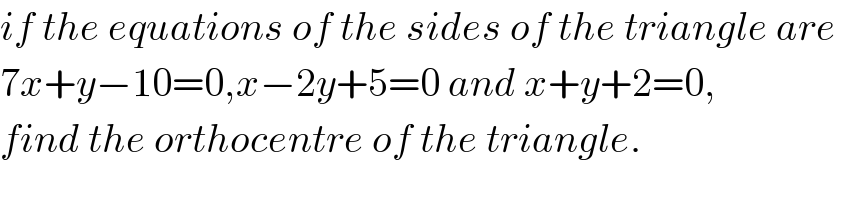
if the equations of the sides of the triangle are 7x+y−10=0,x−2y+5=0 and x+y+2=0, find the orthocentre of the triangle.
$${if}\:{the}\:{equations}\:{of}\:{the}\:{sides}\:{of}\:{the}\:{triangle}\:{are}\: \\ $$$$\mathrm{7}{x}+{y}−\mathrm{10}=\mathrm{0},{x}−\mathrm{2}{y}+\mathrm{5}=\mathrm{0}\:{and}\:{x}+{y}+\mathrm{2}=\mathrm{0}, \\ $$$${find}\:{the}\:{orthocentre}\:{of}\:{the}\:{triangle}. \\ $$
Answered by prakash jain last updated on 16/Mar/15
Lines y=−7x+10 ...(i) y=(1/2)x+(5/2) ...(ii) y=−x−2 ...(iii) Vertices (i) and (ii) x_1 =1, y_1 =3 (ii) and (iii) x_2 =−3, y_2 =1 (iii) and (i) x_3 =2, y_3 =−4 Equation of line perpendicular to (ii) Slope of a perpendicular line −ve reciprocal y=−2x+c Altitude on line (ii) passes thru (x_3 ,y_3 )=(2,−4) Equation of altitude on (ii) y=−2x .....(altitude 1) Equation of line perpendicular to (iii) y=x+c Altitude on line (iii) passes thru (x_1 ,y_1 )=(1,3) Equation of altitude on (iii) y=x+2 .....(altitude 2) Intersection of altitudes gives orthocenter x=−(2/3), y=(4/3)
$$\mathrm{Lines} \\ $$$${y}=−\mathrm{7}{x}+\mathrm{10}\:\:\:\:\:\:…\left(\mathrm{i}\right) \\ $$$${y}=\frac{\mathrm{1}}{\mathrm{2}}{x}+\frac{\mathrm{5}}{\mathrm{2}}\:\:\:\:\:\:\:…\left(\mathrm{ii}\right) \\ $$$${y}=−{x}−\mathrm{2}\:\:\:\:\:\:\:\:\:\:…\left(\mathrm{iii}\right) \\ $$$$\mathrm{Vertices} \\ $$$$\left(\mathrm{i}\right)\:\mathrm{and}\:\left(\mathrm{ii}\right) \\ $$$${x}_{\mathrm{1}} =\mathrm{1},\:{y}_{\mathrm{1}} =\mathrm{3} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{and}\:\left(\mathrm{iii}\right) \\ $$$${x}_{\mathrm{2}} =−\mathrm{3},\:{y}_{\mathrm{2}} =\mathrm{1} \\ $$$$\left(\mathrm{iii}\right)\:\mathrm{and}\:\left(\mathrm{i}\right) \\ $$$${x}_{\mathrm{3}} =\mathrm{2},\:{y}_{\mathrm{3}} =−\mathrm{4} \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{line}\:\mathrm{perpendicular}\:\mathrm{to}\:\left(\mathrm{ii}\right) \\ $$$$\mathrm{Slope}\:\mathrm{of}\:\mathrm{a}\:\mathrm{perpendicular}\:\mathrm{line}\:−\mathrm{ve}\:\mathrm{reciprocal} \\ $$$${y}=−\mathrm{2}{x}+{c} \\ $$$$\mathrm{Altitude}\:\mathrm{on}\:\mathrm{line}\:\left(\mathrm{ii}\right)\:\mathrm{passes}\:\mathrm{thru}\:\left({x}_{\mathrm{3}} ,\mathrm{y}_{\mathrm{3}} \right)=\left(\mathrm{2},−\mathrm{4}\right) \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{altitude}\:\mathrm{on}\:\left(\mathrm{ii}\right) \\ $$$${y}=−\mathrm{2}{x}\:\:\:\:\:\:\:…..\left(\mathrm{altitude}\:\mathrm{1}\right) \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{line}\:\mathrm{perpendicular}\:\mathrm{to}\:\left(\mathrm{iii}\right) \\ $$$${y}={x}+{c} \\ $$$$\mathrm{Altitude}\:\mathrm{on}\:\mathrm{line}\:\left(\mathrm{iii}\right)\:\mathrm{passes}\:\mathrm{thru}\:\left({x}_{\mathrm{1}} ,\mathrm{y}_{\mathrm{1}} \right)=\left(\mathrm{1},\mathrm{3}\right) \\ $$$$\mathrm{Equation}\:\mathrm{of}\:\mathrm{altitude}\:\mathrm{on}\:\left(\mathrm{iii}\right) \\ $$$${y}={x}+\mathrm{2}\:\:\:\:\:\:\:…..\left(\mathrm{altitude}\:\mathrm{2}\right) \\ $$$$\mathrm{Intersection}\:\mathrm{of}\:\mathrm{altitudes}\:\mathrm{gives}\:\mathrm{orthocenter} \\ $$$${x}=−\frac{\mathrm{2}}{\mathrm{3}},\:{y}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *