Question Number 68991 by pranay02 last updated on 17/Sep/19
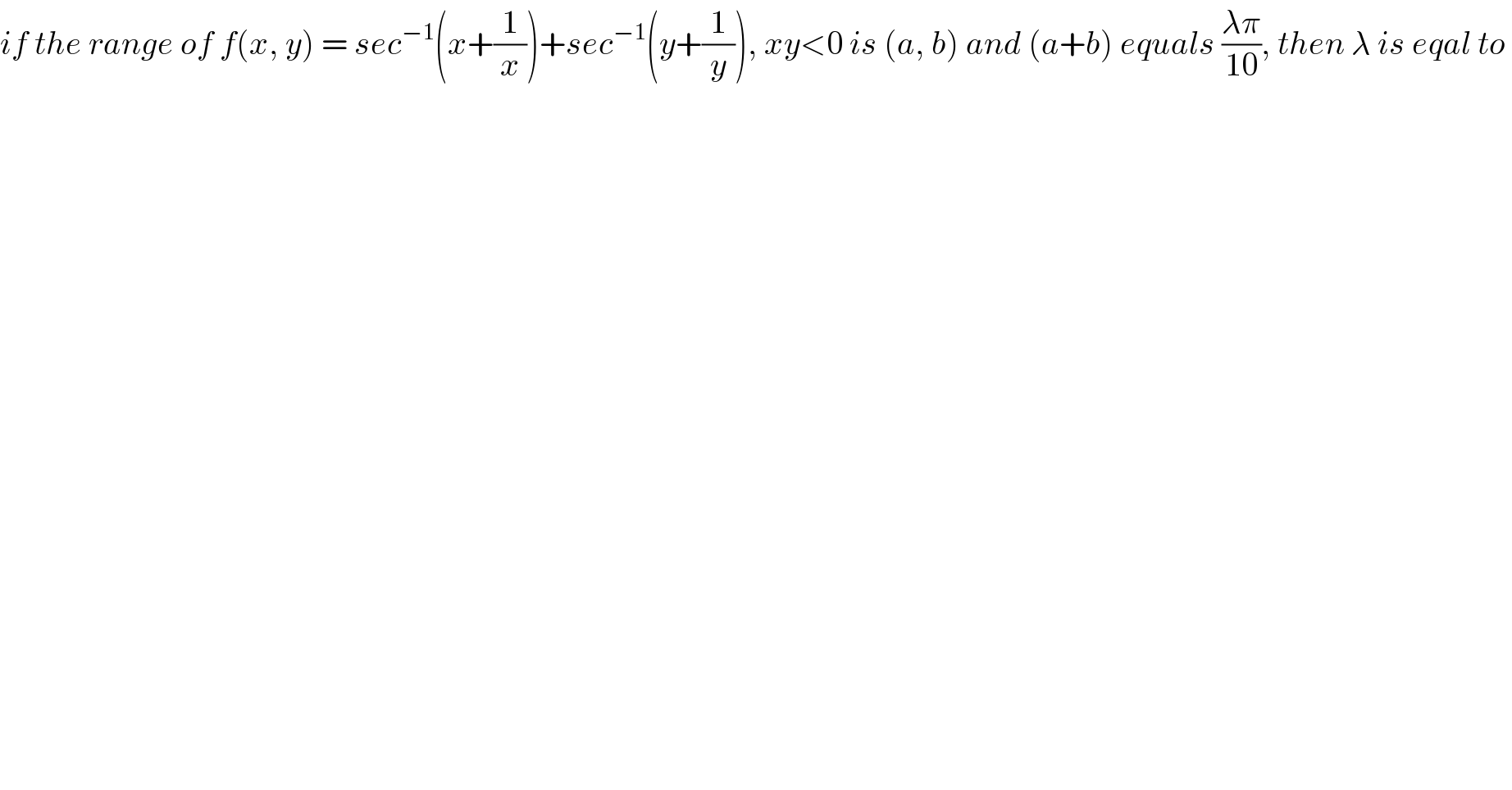
$${if}\:{the}\:{range}\:{of}\:{f}\left({x},\:{y}\right)\:=\:{sec}^{−\mathrm{1}} \left({x}+\frac{\mathrm{1}}{{x}}\right)+{sec}^{−\mathrm{1}} \left({y}+\frac{\mathrm{1}}{{y}}\right),\:{xy}<\mathrm{0}\:{is}\:\left({a},\:{b}\right)\:{and}\:\left({a}+{b}\right)\:{equals}\:\frac{\lambda\pi}{\mathrm{10}},\:{then}\:\lambda\:{is}\:{eqal}\:{to}\: \\ $$
Answered by MJS last updated on 18/Sep/19

$${g}\left({t}\right)=\mathrm{sec}^{−\mathrm{1}} \:\left({t}+\frac{\mathrm{1}}{{t}}\right)\:=\mathrm{cos}^{−\mathrm{1}} \:\left(\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$$$\frac{\pi}{\mathrm{3}}\leqslant{g}\left({t}\right)\leqslant\frac{\mathrm{2}\pi}{\mathrm{3}} \\ $$$$\mathrm{the}\:\mathrm{minimum}\:\mathrm{is}\:\mathrm{at}\:\begin{pmatrix}{\mathrm{1}}\\{\frac{\pi}{\mathrm{3}}}\end{pmatrix} \\ $$$$\mathrm{the}\:\mathrm{maximum}\:\mathrm{is}\:\mathrm{at}\:\begin{pmatrix}{−\mathrm{1}}\\{\frac{\mathrm{2}\pi}{\mathrm{3}}}\end{pmatrix} \\ $$$${t}<\mathrm{0}\:\Rightarrow\:\frac{\pi}{\mathrm{2}}<{g}\left({t}\right)\leqslant\frac{\mathrm{3}\pi}{\mathrm{2}} \\ $$$${t}>\mathrm{0}\:\Rightarrow\:\frac{\pi}{\mathrm{3}}\leqslant{g}\left({t}\right)<\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{5}\pi}{\mathrm{6}}<{f}\left({x},\:{y}\right)<\mathrm{2}\pi\:\mathrm{for}\:{xy}<\mathrm{0} \\ $$$$\frac{\mathrm{5}\pi}{\mathrm{6}}+\mathrm{2}\pi=\frac{\mathrm{17}\pi}{\mathrm{6}}=\frac{\lambda\pi}{\mathrm{10}}\:\Rightarrow\:\lambda=\frac{\mathrm{85}}{\mathrm{3}} \\ $$
