Question Number 76715 by peter frank last updated on 29/Dec/19

$${If}\:{u}={arc}\mathrm{sin}\:\frac{{x}}{{y}}+{arc}\mathrm{tan}\:\frac{{y}}{{x}} \\ $$$${show}\:{that}\: \\ $$$${x}\frac{\partial{u}}{{dx}}+{y}\frac{\partial{u}}{{dy}}=\mathrm{0} \\ $$
Commented by abdomathmax last updated on 30/Dec/19
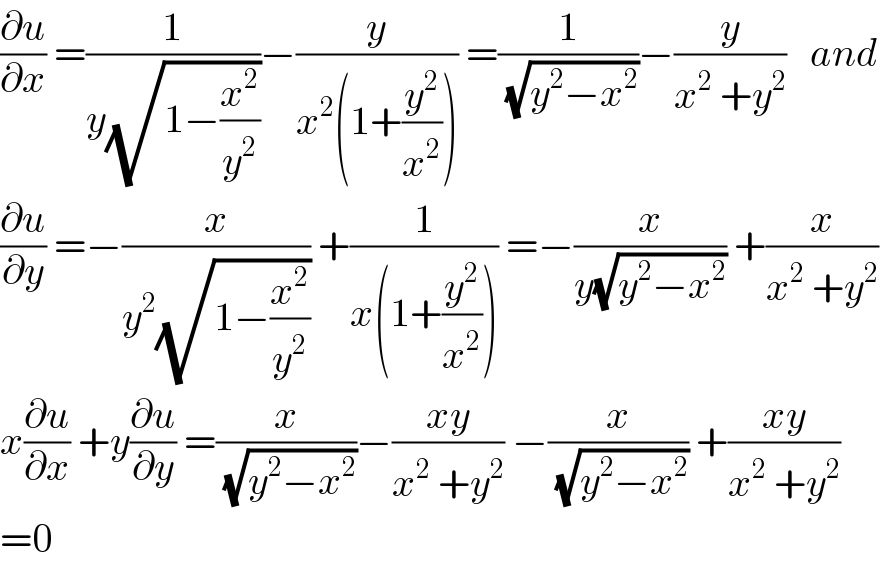
$$\frac{\partial{u}}{\partial{x}}\:=\frac{\mathrm{1}}{{y}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }}}−\frac{{y}}{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}\:=\frac{\mathrm{1}}{\:\sqrt{{y}^{\mathrm{2}} −{x}^{\mathrm{2}} }}−\frac{{y}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:\:\:{and}\: \\ $$$$\frac{\partial{u}}{\partial{y}}\:=−\frac{{x}}{{y}^{\mathrm{2}} \sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }}}\:+\frac{\mathrm{1}}{{x}\left(\mathrm{1}+\frac{{y}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)}\:=−\frac{{x}}{{y}\sqrt{{y}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\:+\frac{{x}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} } \\ $$$${x}\frac{\partial{u}}{\partial{x}}\:+{y}\frac{\partial{u}}{\partial{y}}\:=\frac{{x}}{\:\sqrt{{y}^{\mathrm{2}} −{x}^{\mathrm{2}} }}−\frac{{xy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} }\:−\frac{{x}}{\:\sqrt{{y}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\:+\frac{{xy}}{{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} } \\ $$$$=\mathrm{0} \\ $$
Commented by peter frank last updated on 30/Dec/19

$${help}\:\mathrm{76713} \\ $$
Commented by peter frank last updated on 01/Jan/20

$${thank}\:{you} \\ $$
