Question Number 295 by defg last updated on 25/Jan/15
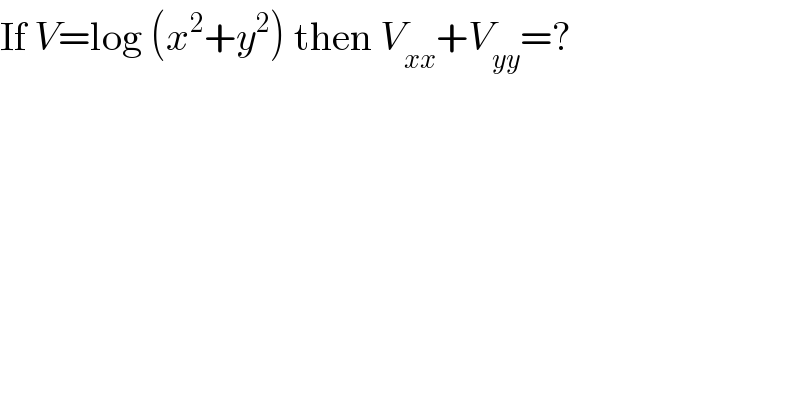
$$\mathrm{If}\:{V}=\mathrm{log}\:\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)\:\mathrm{then}\:{V}_{{xx}} +{V}_{{yy}} =? \\ $$
Answered by 123456 last updated on 19/Dec/14

$${V}_{{x}} =\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${V}_{{xx}} =\frac{\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}{x}\centerdot\mathrm{2}{x}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} } \\ $$$${V}_{{y}} =\frac{\mathrm{2}{y}}{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} } \\ $$$${V}_{{yy}} =\frac{\mathrm{2}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)−\mathrm{2}{y}\centerdot\mathrm{2}{y}}{\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)^{\mathrm{2}} }=\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} } \\ $$$${V}_{{xx}} +{V}_{{yy}} =\frac{−\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} }+\frac{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} }{{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{4}} }=\mathrm{0} \\ $$
