Question Number 72883 by mhmd last updated on 04/Nov/19
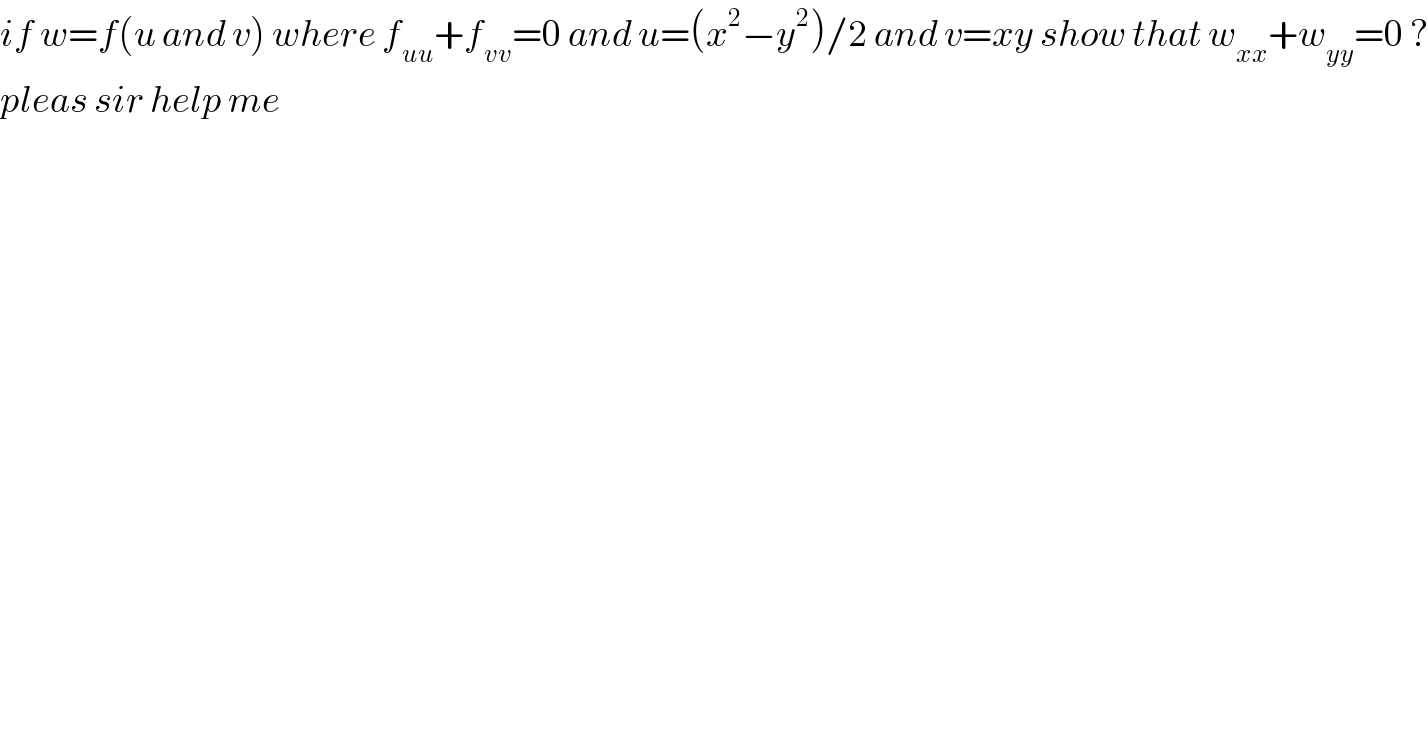
$${if}\:{w}={f}\left({u}\:{and}\:{v}\right)\:{where}\:{f}_{{uu}} +{f}_{{vv}} =\mathrm{0}\:{and}\:{u}=\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)/\mathrm{2}\:{and}\:{v}={xy}\:{show}\:{that}\:{w}_{{xx}} +{w}_{{yy}} =\mathrm{0}\:? \\ $$$${pleas}\:{sir}\:{help}\:{me} \\ $$
Answered by mind is power last updated on 04/Nov/19
![w(x,y)=f(u,v) w(x,y)=f(β(x,y)) ⇒jac W=jac(f).jacβ(x,y) ⇒((∂w/∂x),(∂w/∂y))=((∂f/∂u),(∂f/∂v)). [((x −y)),((y x)) ] ⇒(∂w/∂x)=((x∂f)/∂u)+((y∂f)/∂v) ⇒(∂w/∂y)=−y(∂f/∂u)+x(∂f/∂v) (∂^2 W/∂x^2 )=(∂f/∂u)+x((∂^2 f/∂u^2 ).x+(∂^2 f/(∂u∂v))y)+y((∂^2 f/(∂v∂u))x+(∂^2 f/∂v^2 )y) (∂^2 w/∂y^2 )=−(∂f/∂u)−y((∂^2 f/∂u^2 ).−y+(∂^2 f/(∂u∂v))x)+x((∂^2 f/(∂u∂v)).−y+(∂^2 f/∂v^2 ).x) ⇒(∂^2 w/∂x^2 )=(∂f/∂u)+2xy(∂^2 f/(∂u∂v))+x^2 (∂^2 f/∂u^2 )+y^2 (∂^2 f/∂v^2 ) (∂^2 w/∂y^2 )=−(∂f/∂u)−2xy(∂^2 f/(∂u∂v))+x^2 (∂^2 f/∂v^2 )+y^2 (∂^2 f/∂u^2 ) ⇒(∂^2 w/∂x^2 )+(∂^2 w/∂y^2 )=(x^2 +y^2 )[(∂^2 f/∂u^2 )+(∂^2 f/∂v^2 )]=(x^2 +y^2 ).0=0](https://www.tinkutara.com/question/Q72890.png)
$$\mathrm{w}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{f}\left(\mathrm{u},\mathrm{v}\right) \\ $$$$\mathrm{w}\left(\mathrm{x},\mathrm{y}\right)=\mathrm{f}\left(\beta\left(\mathrm{x},\mathrm{y}\right)\right) \\ $$$$\Rightarrow\mathrm{jac}\:\mathrm{W}=\mathrm{jac}\left(\mathrm{f}\right).\mathrm{jac}\beta\left(\mathrm{x},\mathrm{y}\right) \\ $$$$\:\Rightarrow\left(\frac{\partial\mathrm{w}}{\partial\mathrm{x}},\frac{\partial\mathrm{w}}{\partial\mathrm{y}}\right)=\left(\frac{\partial\mathrm{f}}{\partial\mathrm{u}},\frac{\partial\mathrm{f}}{\partial\mathrm{v}}\right).\begin{bmatrix}{\mathrm{x}\:\:\:\:\:\:\:\:−\mathrm{y}}\\{\mathrm{y}\:\:\:\:\:\mathrm{x}}\end{bmatrix}\: \\ $$$$\Rightarrow\frac{\partial\mathrm{w}}{\partial\mathrm{x}}=\frac{\mathrm{x}\partial\mathrm{f}}{\partial\mathrm{u}}+\frac{\mathrm{y}\partial\mathrm{f}}{\partial\mathrm{v}} \\ $$$$\Rightarrow\frac{\partial\mathrm{w}}{\partial\mathrm{y}}=−\mathrm{y}\frac{\partial\mathrm{f}}{\partial\mathrm{u}}+\mathrm{x}\frac{\partial\mathrm{f}}{\partial\mathrm{v}} \\ $$$$\frac{\partial^{\mathrm{2}} \mathrm{W}}{\partial\mathrm{x}^{\mathrm{2}} }=\frac{\partial\mathrm{f}}{\partial\mathrm{u}}+\mathrm{x}\left(\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}^{\mathrm{2}} }.\mathrm{x}+\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}\partial\mathrm{v}}\mathrm{y}\right)+\mathrm{y}\left(\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{v}\partial\mathrm{u}}\mathrm{x}+\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{v}^{\mathrm{2}} }\mathrm{y}\right) \\ $$$$\frac{\partial^{\mathrm{2}} \mathrm{w}}{\partial\mathrm{y}^{\mathrm{2}} }=−\frac{\partial\mathrm{f}}{\partial\mathrm{u}}−\mathrm{y}\left(\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}^{\mathrm{2}} }.−\mathrm{y}+\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}\partial\mathrm{v}}\mathrm{x}\right)+\mathrm{x}\left(\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}\partial\mathrm{v}}.−\mathrm{y}+\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{v}^{\mathrm{2}} }.\mathrm{x}\right) \\ $$$$\Rightarrow\frac{\partial^{\mathrm{2}} \mathrm{w}}{\partial\mathrm{x}^{\mathrm{2}} }=\frac{\partial\mathrm{f}}{\partial\mathrm{u}}+\mathrm{2xy}\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}\partial\mathrm{v}}+\mathrm{x}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}^{\mathrm{2}} }+\mathrm{y}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{v}^{\mathrm{2}} } \\ $$$$\frac{\partial^{\mathrm{2}} \mathrm{w}}{\partial\mathrm{y}^{\mathrm{2}} }=−\frac{\partial\mathrm{f}}{\partial\mathrm{u}}−\mathrm{2xy}\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}\partial\mathrm{v}}+\mathrm{x}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{v}^{\mathrm{2}} }+\mathrm{y}^{\mathrm{2}} \frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}^{\mathrm{2}} } \\ $$$$\Rightarrow\frac{\partial^{\mathrm{2}} \mathrm{w}}{\partial\mathrm{x}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} \mathrm{w}}{\partial\mathrm{y}^{\mathrm{2}} }=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right)\left[\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{u}^{\mathrm{2}} }+\frac{\partial^{\mathrm{2}} \mathrm{f}}{\partial\mathrm{v}^{\mathrm{2}} }\right]=\left(\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} \right).\mathrm{0}=\mathrm{0} \\ $$
