Menu Close

if-x-0-then-prove-x-4-x-4-1-x-3-x-3-x-2-1-x-x-x-2-1-

Tinku Tara 0 Comments
Pin




Question Number 8016 by Nayon last updated on 28/Sep/16
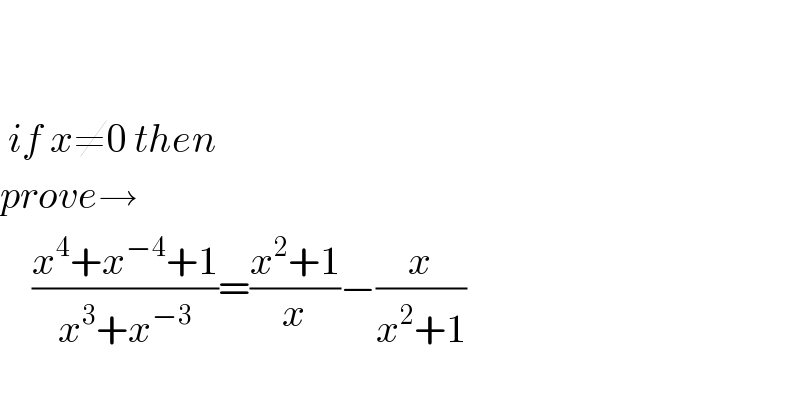
if x≠0 then prove→ ((x^4 +x^(−4) +1)/(x^3 +x^(−3) ))=((x^2 +1)/x)−(x/(x^2 +1))
$$ \\ $$$$ \\ $$$$\:{if}\:{x}\neq\mathrm{0}\:{then} \\ $$$${prove}\rightarrow \\ $$$$\:\:\:\:\frac{{x}^{\mathrm{4}} +{x}^{−\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{3}} +{x}^{−\mathrm{3}} }=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}−\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$
Commented by FilupSmith last updated on 28/Sep/16
((x^4 +(1/x^4 )+1)/(x^3 +(1/x^3 )))=(((x^8 +1+x^4 )/x^4 )/((x^6 +1)/x^3 )) =((x^8 +x^4 +1)/x^4 )+(x^3 /(x^6 +1)) =x^4 +1+(1/x^4 )+(x^3 /(x^6 +1)) continue
$$\frac{{x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\mathrm{1}}{{x}^{\mathrm{3}} +\frac{\mathrm{1}}{{x}^{\mathrm{3}} }}=\frac{\frac{{x}^{\mathrm{8}} +\mathrm{1}+{x}^{\mathrm{4}} }{{x}^{\mathrm{4}} }}{\frac{{x}^{\mathrm{6}} +\mathrm{1}}{{x}^{\mathrm{3}} }} \\ $$$$=\frac{{x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{6}} +\mathrm{1}} \\ $$$$={x}^{\mathrm{4}} +\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{4}} }+\frac{{x}^{\mathrm{3}} }{{x}^{\mathrm{6}} +\mathrm{1}} \\ $$$${continue} \\ $$
Commented by Nayon last updated on 28/Sep/16
wrong way filup
$${wrong}\:{way}\:{filup}\: \\ $$
Answered by Rasheed Soomro last updated on 28/Sep/16
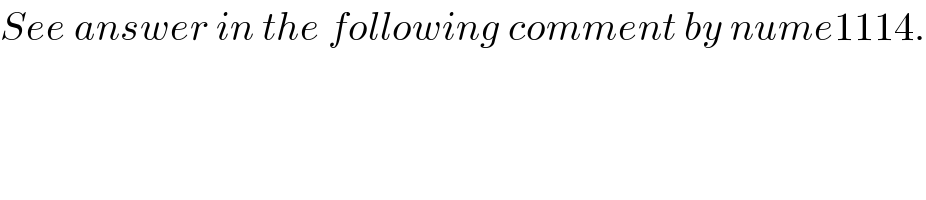
See answer in the following comment by nume1114.
$${See}\:{answer}\:{in}\:{the}\:{following}\:{comment}\:{by}\:{nume}\mathrm{1114}. \\ $$
Commented by Nayon last updated on 28/Sep/16
the question is that to prove it. it′s a identity, not only a equetion.
$${the}\:{question}\:{is}\:{that}\:{to}\:{prove}\:{it}.\:{it}'{s}\:{a}\:{identity}, \\ $$$${not}\:{only}\:{a}\:{equetion}. \\ $$
Commented by Rasheed Soomro last updated on 28/Sep/16
Sorry I misread.
$${Sorry}\:{I}\:{misread}. \\ $$
Commented by nume1114 last updated on 28/Sep/16
Let x+x^(−1) =y x^2 +x^(−2) =y^2 −2 x^3 +x^(−3) =y^3 −3y x^4 +x^(−4) =y^4 −4y^2 +2 LHS=((y^4 −4y^2 +3)/(y^3 −3y))=(((y^2 −3)(y^2 −1))/(y(y^2 −3))) [((if x>0)),((y=x+x^(−1) ≥2(√(xx^(−1) ))=2)),((if x<0)),((−y=−x+(−x)^(−1) ≥2(√((−x)∙(−x^(−1) )))=2)),((y≤−2)),((so,y^2 −3≠0)) ] (((y^2 −3)(y^2 −1))/(y(y^2 −3)))=((y^2 −1)/y)=y−(1/y) =x+(1/x)−(1/(x+(1/x)))=RHS Proved
$${Let}\:{x}+{x}^{−\mathrm{1}} ={y} \\ $$$${x}^{\mathrm{2}} +{x}^{−\mathrm{2}} ={y}^{\mathrm{2}} −\mathrm{2} \\ $$$${x}^{\mathrm{3}} +{x}^{−\mathrm{3}} ={y}^{\mathrm{3}} −\mathrm{3}{y} \\ $$$${x}^{\mathrm{4}} +{x}^{−\mathrm{4}} ={y}^{\mathrm{4}} −\mathrm{4}{y}^{\mathrm{2}} +\mathrm{2} \\ $$$${LHS}=\frac{{y}^{\mathrm{4}} −\mathrm{4}{y}^{\mathrm{2}} +\mathrm{3}}{{y}^{\mathrm{3}} −\mathrm{3}{y}}=\frac{\left({y}^{\mathrm{2}} −\mathrm{3}\right)\left({y}^{\mathrm{2}} −\mathrm{1}\right)}{{y}\left({y}^{\mathrm{2}} −\mathrm{3}\right)} \\ $$$$\:\:\:\begin{bmatrix}{{if}\:{x}>\mathrm{0}}\\{{y}={x}+{x}^{−\mathrm{1}} \geqslant\mathrm{2}\sqrt{{xx}^{−\mathrm{1}} }=\mathrm{2}}\\{{if}\:{x}<\mathrm{0}}\\{−{y}=−{x}+\left(−{x}\right)^{−\mathrm{1}} \geqslant\mathrm{2}\sqrt{\left(−{x}\right)\centerdot\left(−{x}^{−\mathrm{1}} \right)}=\mathrm{2}}\\{{y}\leqslant−\mathrm{2}}\\{{so},{y}^{\mathrm{2}} −\mathrm{3}\neq\mathrm{0}}\end{bmatrix} \\ $$$$\:\:\:\:\frac{\left({y}^{\mathrm{2}} −\mathrm{3}\right)\left({y}^{\mathrm{2}} −\mathrm{1}\right)}{{y}\left({y}^{\mathrm{2}} −\mathrm{3}\right)}=\frac{{y}^{\mathrm{2}} −\mathrm{1}}{{y}}={y}−\frac{\mathrm{1}}{{y}} \\ $$$$={x}+\frac{\mathrm{1}}{{x}}−\frac{\mathrm{1}}{{x}+\frac{\mathrm{1}}{{x}}}={RHS} \\ $$$${Proved} \\ $$
Answered by sandy_suhendra last updated on 28/Sep/16
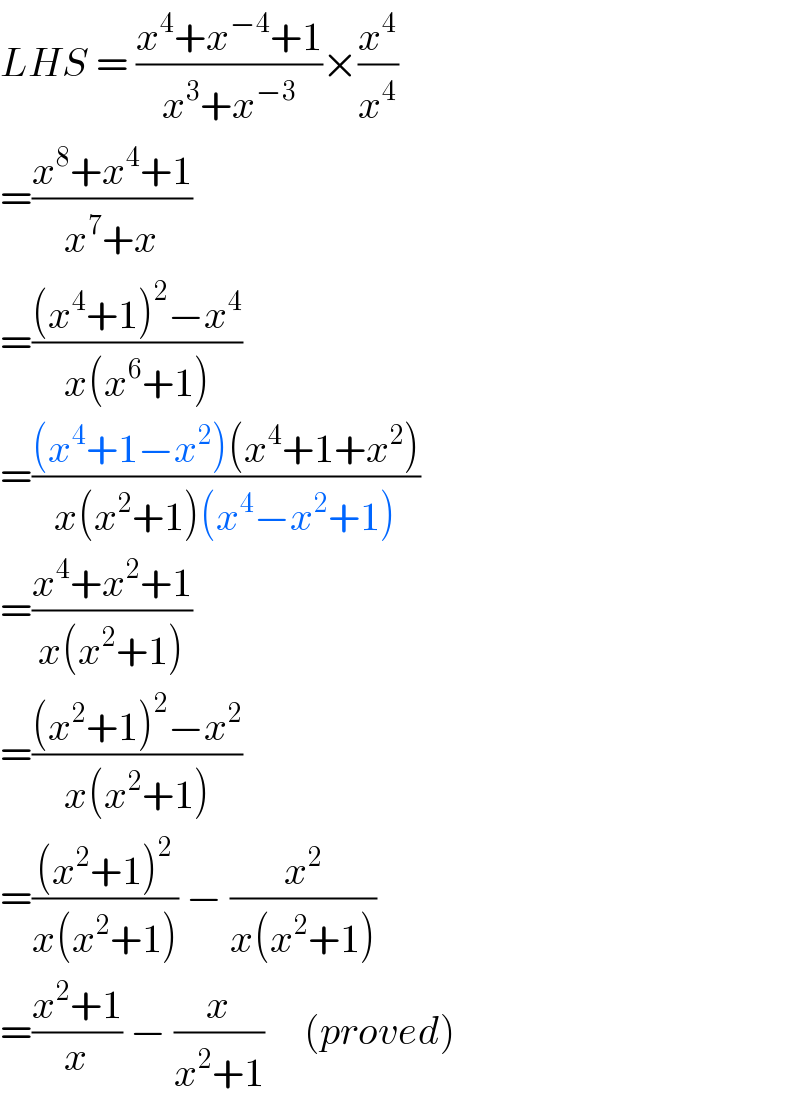
LHS = ((x^4 +x^(−4) +1)/(x^3 +x^(−3) ))×(x^4 /x^4 ) =((x^8 +x^4 +1)/(x^7 +x)) =(((x^4 +1)^2 −x^4 )/(x(x^6 +1))) =(((x^4 +1−x^2 )(x^4 +1+x^2 ))/(x(x^2 +1)(x^4 −x^2 +1))) =((x^4 +x^2 +1)/(x(x^2 +1))) =(((x^2 +1)^2 −x^2 )/(x(x^2 +1))) =(((x^2 +1)^2 )/(x(x^2 +1))) − (x^2 /(x(x^2 +1))) =((x^2 +1)/x) − (x/(x^2 +1)) (proved)
$${LHS}\:=\:\frac{{x}^{\mathrm{4}} +{x}^{−\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{3}} +{x}^{−\mathrm{3}} }×\frac{{x}^{\mathrm{4}} }{{x}^{\mathrm{4}} } \\ $$$$=\frac{{x}^{\mathrm{8}} +{x}^{\mathrm{4}} +\mathrm{1}}{{x}^{\mathrm{7}} +{x}} \\ $$$$=\frac{\left({x}^{\mathrm{4}} +\mathrm{1}\right)^{\mathrm{2}} −{x}^{\mathrm{4}} }{{x}\left({x}^{\mathrm{6}} +\mathrm{1}\right)} \\ $$$$=\frac{\left({x}^{\mathrm{4}} +\mathrm{1}−{x}^{\mathrm{2}} \right)\left({x}^{\mathrm{4}} +\mathrm{1}+{x}^{\mathrm{2}} \right)}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\left({x}^{\mathrm{4}} −{x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} +\mathrm{1}}{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} }{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\:−\:\frac{{x}^{\mathrm{2}} }{{x}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$$$=\frac{{x}^{\mathrm{2}} +\mathrm{1}}{{x}}\:−\:\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\:\:\:\:\:\left({proved}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *