Menu Close

If-x-1-x-1-find-out-value-x-20-x-17-x-14-x-11-x-17-x-14-x-11-x-8-

Tinku Tara 0 Comments
Pin




Question Number 66058 by arvinddayama01@gmail.comm last updated on 08/Aug/19
If x + (1/x)=1 find out value:− ((x^(20) +x^(17) +x^(14) +x^(11) )/(x^(17) +x^(14) +x^(11) +x^8 )) = ?
$${If}\:\:\:\:{x}\:+\:\frac{\mathrm{1}}{{x}}=\mathrm{1} \\ $$$$ \\ $$$${find}\:{out}\:{value}:− \\ $$$$ \\ $$$$\:\:\:\:\frac{{x}^{\mathrm{20}} +{x}^{\mathrm{17}} +{x}^{\mathrm{14}} +{x}^{\mathrm{11}} }{{x}^{\mathrm{17}} +{x}^{\mathrm{14}} +{x}^{\mathrm{11}} +{x}^{\mathrm{8}} }\:\:\:\:=\:\:\:\:? \\ $$
Commented by Prithwish sen last updated on 08/Aug/19
x^2 −x+1=0⇒(x+1)(x^2 −x+1)=0⇒x^3 =−1 ((x^3 (x^(17) +x^(14) +x^(11) +x^8 ))/(x^(17) +x^(14) +x^(11) +x^8 )) = x^3 = −1
$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\Rightarrow\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)=\mathrm{0}\Rightarrow\mathrm{x}^{\mathrm{3}} =−\mathrm{1} \\ $$$$\frac{\mathrm{x}^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{17}} +\mathrm{x}^{\mathrm{14}} +\mathrm{x}^{\mathrm{11}} +\mathrm{x}^{\mathrm{8}} \right)}{\mathrm{x}^{\mathrm{17}} +\mathrm{x}^{\mathrm{14}} +\mathrm{x}^{\mathrm{11}} +\mathrm{x}^{\mathrm{8}} }\:=\:\mathrm{x}^{\mathrm{3}} \:=\:−\mathrm{1} \\ $$
Commented by $@ty@m123 last updated on 08/Aug/19
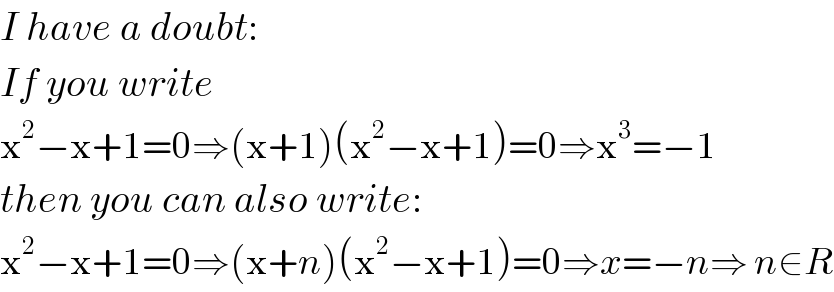
I have a doubt: If you write x^2 −x+1=0⇒(x+1)(x^2 −x+1)=0⇒x^3 =−1 then you can also write: x^2 −x+1=0⇒(x+n)(x^2 −x+1)=0⇒x=−n⇒ n∈R
$${I}\:{have}\:{a}\:{doubt}: \\ $$$${If}\:{you}\:{write} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\Rightarrow\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)=\mathrm{0}\Rightarrow\mathrm{x}^{\mathrm{3}} =−\mathrm{1} \\ $$$${then}\:{you}\:{can}\:{also}\:{write}: \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\Rightarrow\left(\mathrm{x}+{n}\right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right)=\mathrm{0}\Rightarrow{x}=−{n}\Rightarrow\:{n}\in{R} \\ $$
Commented by Prithwish sen last updated on 08/Aug/19
I have just used the formula of a^3 +b^3 =(a+b)(a^2 −ab+b^2 ) where I just put a=x and b = 1.
$$\mathrm{I}\:\mathrm{have}\:\mathrm{just}\:\mathrm{used}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{of} \\ $$$$\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} =\left(\mathrm{a}+\mathrm{b}\right)\left(\mathrm{a}^{\mathrm{2}} −\mathrm{ab}+\mathrm{b}^{\mathrm{2}} \right)\:\mathrm{where}\:\mathrm{I}\:\mathrm{just}\: \\ $$$$\mathrm{put}\:\mathrm{a}=\mathrm{x}\:\mathrm{and}\:\mathrm{b}\:=\:\mathrm{1}. \\ $$
Commented by Prithwish sen last updated on 09/Aug/19
I think the equation x^3 +1=0 has 3 roots they are −1,((1±(√3)i)/(2.)) Now x+1=0 has the root x= −1 and x^2 −x+1=0 has two roots ((1±(√3)i)/2) just like the equation x^2 −5x+6=0 has 2 roots 2 and 3 of which x−2=0 is satisfied by x=2 and x−3= 0 is satisfied by x= 3.But as a total the entire equation is satisfied by both 2 roots.
$$\mathrm{I}\:\mathrm{think}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{x}^{\mathrm{3}} +\mathrm{1}=\mathrm{0}\:\mathrm{has}\:\mathrm{3}\: \\ $$$$\mathrm{roots}\:\mathrm{they}\:\mathrm{are}\:−\mathrm{1},\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{2}.} \\ $$$$\mathrm{Now}\:\mathrm{x}+\mathrm{1}=\mathrm{0}\:\mathrm{has}\:\mathrm{the}\:\mathrm{root}\:\mathrm{x}=\:−\mathrm{1} \\ $$$$\mathrm{and}\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}=\mathrm{0}\:\mathrm{has}\:\mathrm{two}\:\mathrm{roots}\:\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}\mathrm{i}}{\mathrm{2}} \\ $$$$\mathrm{just}\:\mathrm{like}\:\mathrm{the}\:\mathrm{equation}\: \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{5x}+\mathrm{6}=\mathrm{0}\:\mathrm{has}\:\mathrm{2}\:\mathrm{roots}\:\mathrm{2}\:\mathrm{and}\:\mathrm{3} \\ $$$$\mathrm{of}\:\mathrm{which}\:\mathrm{x}−\mathrm{2}=\mathrm{0}\:\mathrm{is}\:\mathrm{satisfied}\:\mathrm{by}\:\mathrm{x}=\mathrm{2} \\ $$$$\mathrm{and}\:\mathrm{x}−\mathrm{3}=\:\mathrm{0}\:\mathrm{is}\:\mathrm{satisfied}\:\mathrm{by}\:\mathrm{x}=\:\mathrm{3}.\mathrm{But}\:\mathrm{as}\:\mathrm{a}\:\mathrm{total} \\ $$$$\mathrm{the}\:\mathrm{entire}\:\mathrm{equation}\:\mathrm{is}\:\mathrm{satisfied}\:\mathrm{by}\:\mathrm{both}\:\mathrm{2}\: \\ $$$$\mathrm{roots}. \\ $$
Commented by $@ty@m123 last updated on 09/Aug/19
One more observation: The given expression≠x^3 when x=−1
$${One}\:{more}\:{observation}: \\ $$$${The}\:{given}\:{expression}\neq{x}^{\mathrm{3}} \\ $$$${when}\:{x}=−\mathrm{1} \\ $$
Answered by $@ty@m123 last updated on 08/Aug/19
x+(1/x)=1 x^2 −x+1=0 x=((1±(√3)i)/2) The given expression=x^3 =(((1±(√3)i)/2))^3 =(1/8){1±((√3)i)^3 ±3(√3)i+3.(−3)} =(1/8)(1∓3(√3)i∓3(√3)i−9) =((−8)/8) =−1
$${x}+\frac{\mathrm{1}}{{x}}=\mathrm{1} \\ $$$${x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}{i}}{\mathrm{2}} \\ $$$${The}\:{given}\:{expression}={x}^{\mathrm{3}} \\ $$$$=\left(\frac{\mathrm{1}\pm\sqrt{\mathrm{3}}{i}}{\mathrm{2}}\right)^{\mathrm{3}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left\{\mathrm{1}\pm\left(\sqrt{\mathrm{3}}{i}\right)^{\mathrm{3}} \pm\mathrm{3}\sqrt{\mathrm{3}}{i}+\mathrm{3}.\left(−\mathrm{3}\right)\right\} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{1}\mp\mathrm{3}\sqrt{\mathrm{3}}{i}\mp\mathrm{3}\sqrt{\mathrm{3}}{i}−\mathrm{9}\right) \\ $$$$=\frac{−\mathrm{8}}{\mathrm{8}} \\ $$$$=−\mathrm{1} \\ $$
Answered by afjyormathchamp@gmail.com last updated on 08/Aug/19
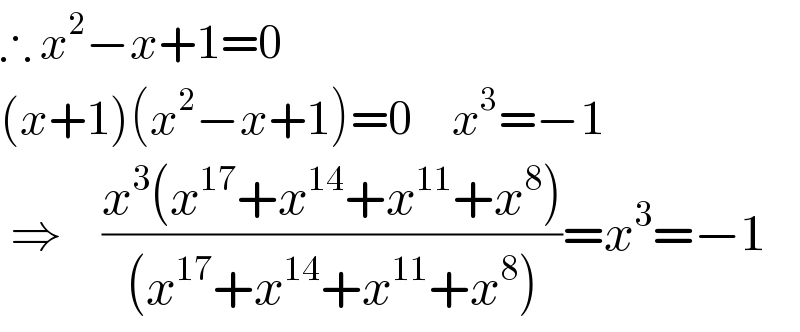
∴ x^2 −x+1=0 (x+1)(x^2 −x+1)=0 x^3 =−1 ⇒ ((x^3 (x^(17) +x^(14) +x^(11) +x^8 ))/((x^(17) +x^(14) +x^(11) +x^8 )))=x^3 =−1
$$\therefore\:{x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)=\mathrm{0}\:\:\:\:\:{x}^{\mathrm{3}} =−\mathrm{1} \\ $$$$\:\Rightarrow\:\:\:\:\frac{{x}^{\mathrm{3}} \left({x}^{\mathrm{17}} +{x}^{\mathrm{14}} +{x}^{\mathrm{11}} +{x}^{\mathrm{8}} \right)}{\left({x}^{\mathrm{17}} +{x}^{\mathrm{14}} +{x}^{\mathrm{11}} +{x}^{\mathrm{8}} \right)}={x}^{\mathrm{3}} =−\mathrm{1} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *