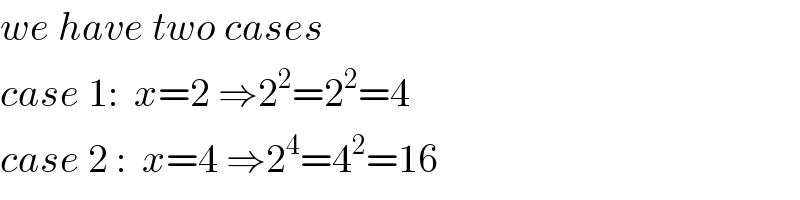If-x-2-2-x-find-x-please-i-need-workings-

Question Number 6216 by sanusihammed last updated on 18/Jun/16

I f x^{2} = 2^{x} f i n d x

p l e a s e i n e e d w o r k i n g s

Answered by prakash jain last updated on 18/Jun/16

2 \ln x = x \ln 2

\frac{\ln 2}{2} = \frac{\ln x}{x} \dots . . (A)

\frac{1}{2} \ln 2 = \frac{\ln x}{e^{\ln x}}

\frac{1}{2} \ln 2 = (\ln x) e^{- \ln x}

- \frac{1}{2} \ln 2 = (- \ln x) e^{- \ln x}

W (- \frac{1}{2} \ln 2) = - \ln x \dots . . (1)

c a l c u l a t i n g W (- \frac{1}{2} \ln 2)

(\ln \frac{1}{2}) e^{\ln \frac{1}{2}} = \frac{1}{2} \ln \frac{1}{2} = \frac{1}{2} (- \ln 2) = - \frac{1}{2} \ln 2

\Rightarrow W (- \frac{1}{2} \ln 2) = \ln \frac{1}{2} \dots . (2)

substituting W (- \frac{1}{2} \ln 2) = \ln \frac{1}{2} from (2) to (1)

\ln \frac{1}{2} = - \ln x \Rightarrow x = 2

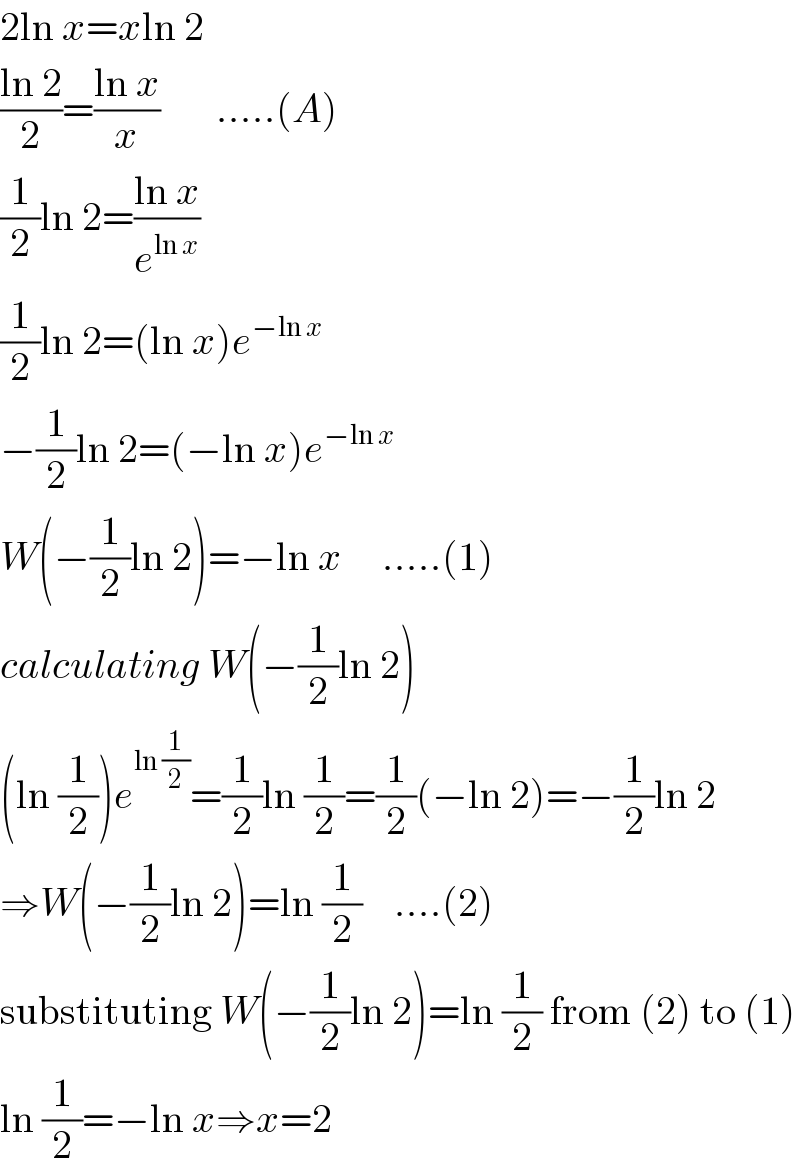
Commented by sanusihammed last updated on 18/Jun/16

T h a n k s .

Commented by FilupSmith last updated on 19/Jun/16

Wow I am having trouble understanding

the last half, good work!

Commented by malwaan last updated on 19/Jun/16

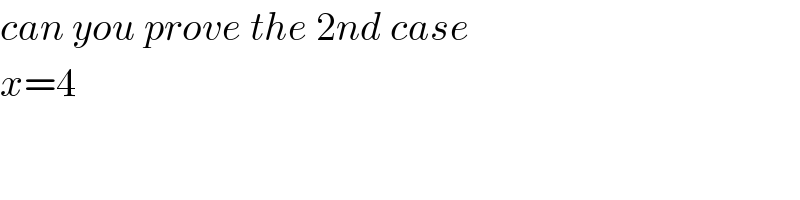
c a n y o u p r o v e t h e 2 n d c a s e

x = 4

Commented by prakash jain last updated on 19/Jun/16

\ln \frac{1}{4} e^{\ln \frac{1}{4}} = \frac{1}{4} \ln \frac{1}{4} = \frac{1}{2} \ln \frac{1}{2} = - \frac{1}{2} \ln 2

W (- \frac{1}{2} \ln 2) is multivalued

W (- \frac{1}{2} \ln 2) = \ln \frac{1}{2} or \ln \frac{1}{4}

x = 2 o r 4

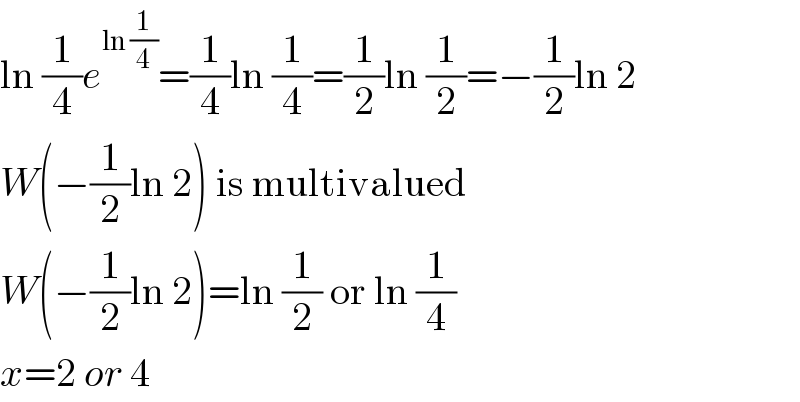
Answered by malwaan last updated on 19/Jun/16

w e h a v e t w o c a s e s

c a s e 1 : x = 2 \Rightarrow 2^{2} = 2^{2} = 4

c a s e 2 : x = 4 \Rightarrow 2^{4} = 4^{2} = 16

Facebook Tweet Pin