Question Number 138367 by KwesiDerek last updated on 12/Apr/21
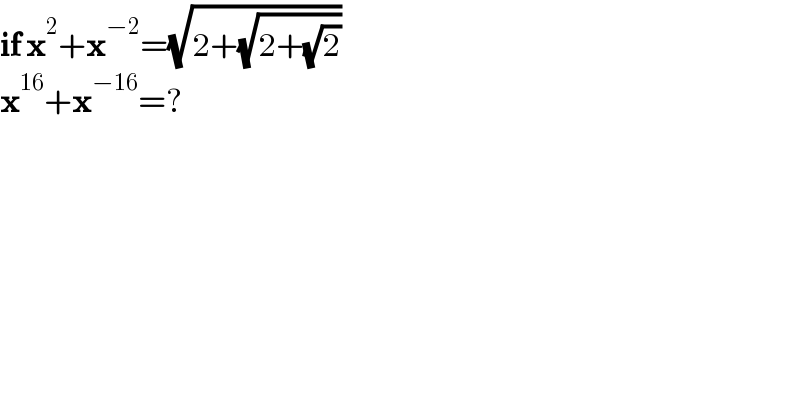
$$\boldsymbol{\mathrm{if}}\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{−\mathrm{2}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{16}} +\boldsymbol{\mathrm{x}}^{−\mathrm{16}} =? \\ $$
Commented by Kamel last updated on 12/Apr/21
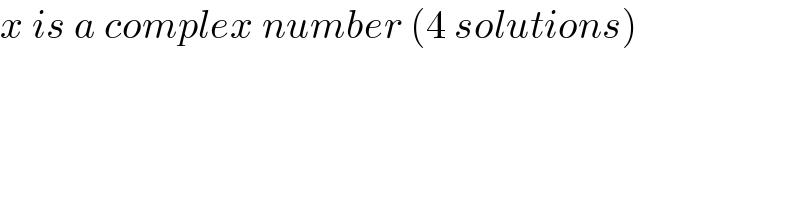
$${x}\:{is}\:{a}\:{complex}\:{number}\:\left(\mathrm{4}\:{solutions}\right) \\ $$
Answered by Kamel last updated on 12/Apr/21
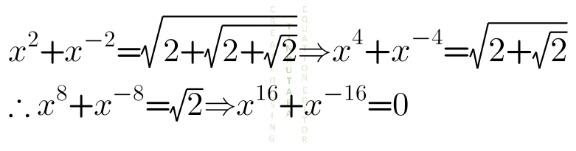
Answered by cherokeesay last updated on 12/Apr/21
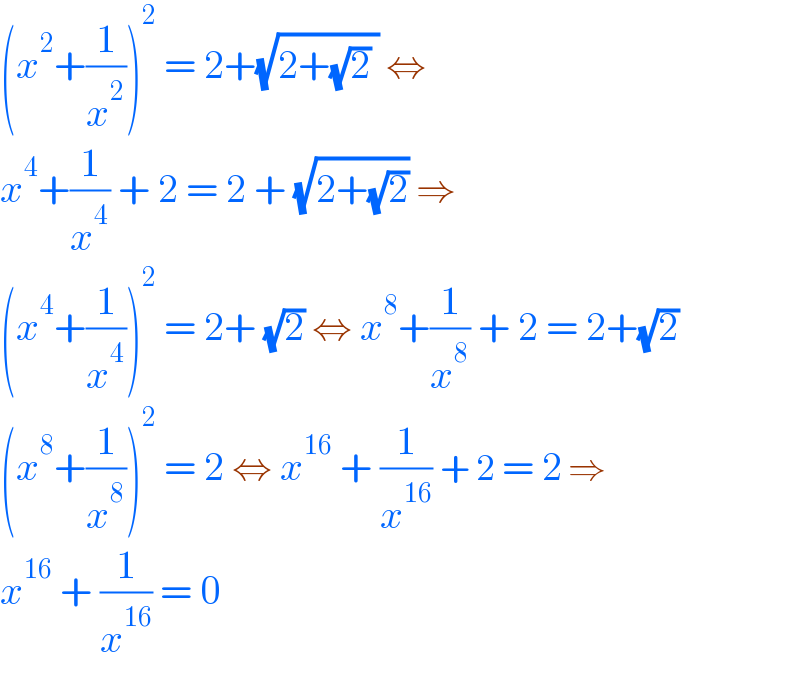
$$\left({x}^{\mathrm{2}} +\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)^{\mathrm{2}} \:=\:\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}\:}\:\Leftrightarrow \\ $$$${x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\:+\:\mathrm{2}\:=\:\mathrm{2}\:+\:\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}\:\Rightarrow\: \\ $$$$\left({x}^{\mathrm{4}} +\frac{\mathrm{1}}{{x}^{\mathrm{4}} }\right)^{\mathrm{2}} \:=\:\mathrm{2}+\:\sqrt{\mathrm{2}}\:\Leftrightarrow\:{x}^{\mathrm{8}} +\frac{\mathrm{1}}{{x}^{\mathrm{8}} }\:+\:\mathrm{2}\:=\:\mathrm{2}+\sqrt{\mathrm{2}} \\ $$$$\left({x}^{\mathrm{8}} +\frac{\mathrm{1}}{{x}^{\mathrm{8}} }\right)^{\mathrm{2}} \:=\:\mathrm{2}\:\Leftrightarrow\:{x}^{\mathrm{16}} \:+\:\frac{\mathrm{1}}{{x}^{\mathrm{16}} }\:+\:\mathrm{2}\:=\:\mathrm{2}\:\Rightarrow \\ $$$${x}^{\mathrm{16}} \:+\:\frac{\mathrm{1}}{{x}^{\mathrm{16}} }\:=\:\mathrm{0} \\ $$
