Question Number 138366 by KwesiDerek last updated on 12/Apr/21
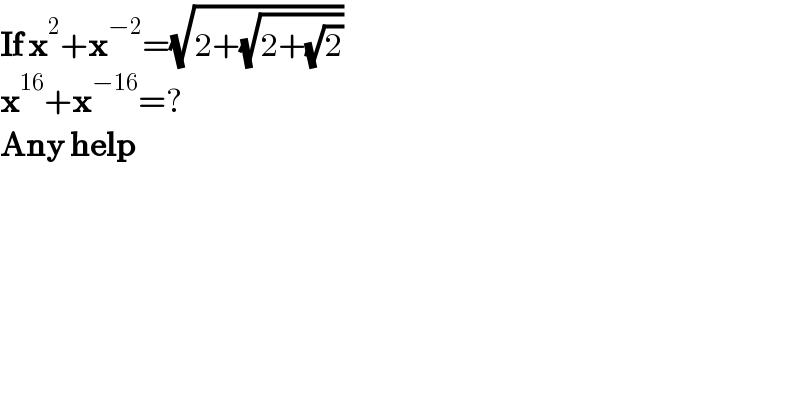
$$\boldsymbol{\mathrm{If}}\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{−\mathrm{2}} =\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}} \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{16}} +\boldsymbol{\mathrm{x}}^{−\mathrm{16}} =? \\ $$$$\boldsymbol{\mathrm{Any}}\:\boldsymbol{\mathrm{help}} \\ $$
Answered by TheSupreme last updated on 14/Apr/21
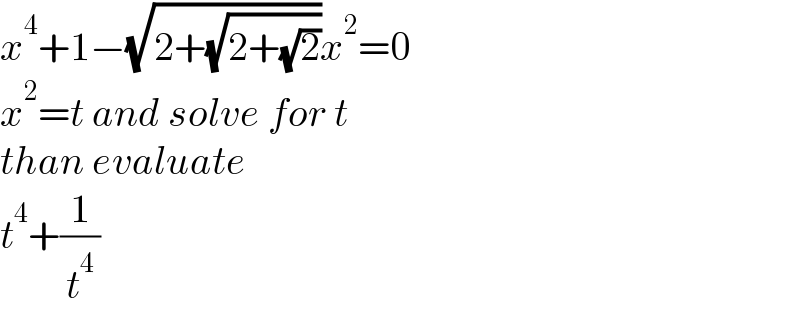
$${x}^{\mathrm{4}} +\mathrm{1}−\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}}}{x}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}^{\mathrm{2}} ={t}\:{and}\:{solve}\:{for}\:{t} \\ $$$${than}\:{evaluate} \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{1}}{{t}^{\mathrm{4}} } \\ $$
Answered by Ñï= last updated on 14/Apr/21
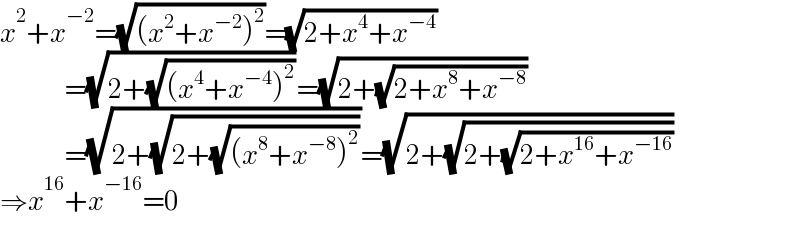
$${x}^{\mathrm{2}} +{x}^{−\mathrm{2}} =\sqrt{\left({x}^{\mathrm{2}} +{x}^{−\mathrm{2}} \right)^{\mathrm{2}} }=\sqrt{\mathrm{2}+{x}^{\mathrm{4}} +{x}^{−\mathrm{4}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}+\sqrt{\left({x}^{\mathrm{4}} +{x}^{−\mathrm{4}} \right)^{\mathrm{2}} }}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+{x}^{\mathrm{8}} +{x}^{−\mathrm{8}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\left({x}^{\mathrm{8}} +{x}^{−\mathrm{8}} \right)^{\mathrm{2}} }}}=\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+\sqrt{\mathrm{2}+{x}^{\mathrm{16}} +{x}^{−\mathrm{16}} }}} \\ $$$$\Rightarrow{x}^{\mathrm{16}} +{x}^{−\mathrm{16}} =\mathrm{0} \\ $$
