Menu Close

If-x-2-xy-y-2-0-find-x-x-y-2023-y-x-y-2023-

Tinku Tara 0 Comments
Pin




Question Number 139948 by qaz last updated on 02/May/21
If x^2 +xy+y^2 =0 find :: ((x/(x+y)))^(2023) +((y/(x+y)))^(2023)
$${If}\:\:\:\:{x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} =\mathrm{0} \\ $$$${find}\:::\:\:\:\left(\frac{{x}}{{x}+{y}}\right)^{\mathrm{2023}} +\left(\frac{{y}}{{x}+{y}}\right)^{\mathrm{2023}} \\ $$
Answered by Rasheed.Sindhi last updated on 04/May/21
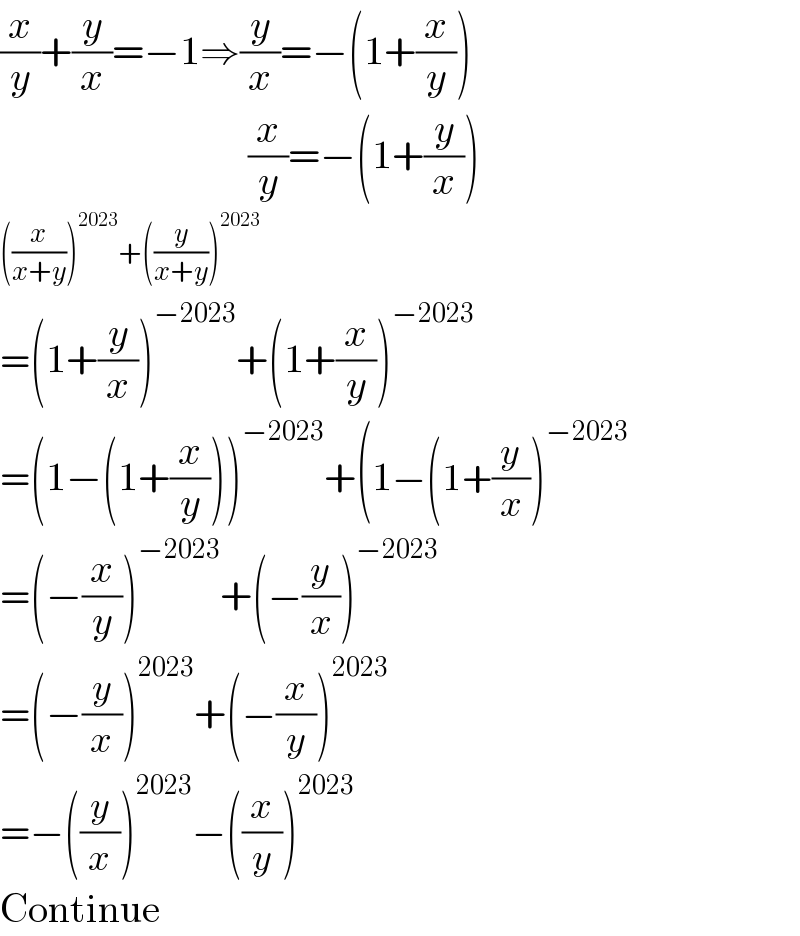
(x/y)+(y/x)=−1⇒(y/x)=−(1+(x/y)) (x/y)=−(1+(y/x)) ((x/(x+y)))^(2023) +((y/(x+y)))^(2023) =(1+(y/x))^(−2023) +(1+(x/y))^(−2023) =(1−(1+(x/y)))^(−2023) +(1−(1+(y/x))^(−2023) =(−(x/y))^(−2023) +(−(y/x))^(−2023) =(−(y/x))^(2023) +(−(x/y))^(2023) =−((y/x))^(2023) −((x/y))^(2023) Continue
$$\frac{{x}}{{y}}+\frac{{y}}{{x}}=−\mathrm{1}\Rightarrow\frac{{y}}{{x}}=−\left(\mathrm{1}+\frac{{x}}{{y}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{{x}}{{y}}=−\left(\mathrm{1}+\frac{{y}}{{x}}\right) \\ $$$$\left(\frac{{x}}{{x}+{y}}\right)^{\mathrm{2023}} +\left(\frac{{y}}{{x}+{y}}\right)^{\mathrm{2023}} \\ $$$$=\left(\mathrm{1}+\frac{{y}}{{x}}\right)^{−\mathrm{2023}} +\left(\mathrm{1}+\frac{{x}}{{y}}\right)^{−\mathrm{2023}} \\ $$$$=\left(\mathrm{1}−\left(\mathrm{1}+\frac{{x}}{{y}}\right)\right)^{−\mathrm{2023}} +\left(\mathrm{1}−\left(\mathrm{1}+\frac{{y}}{{x}}\right)^{−\mathrm{2023}} \right. \\ $$$$=\left(−\frac{{x}}{{y}}\right)^{−\mathrm{2023}} +\left(−\frac{{y}}{{x}}\right)^{−\mathrm{2023}} \\ $$$$=\left(−\frac{{y}}{{x}}\right)^{\mathrm{2023}} +\left(−\frac{{x}}{{y}}\right)^{\mathrm{2023}} \\ $$$$=−\left(\frac{{y}}{{x}}\right)^{\mathrm{2023}} −\left(\frac{{x}}{{y}}\right)^{\mathrm{2023}} \\ $$$$\mathrm{Continue} \\ $$
Answered by mathmax by abdo last updated on 02/May/21
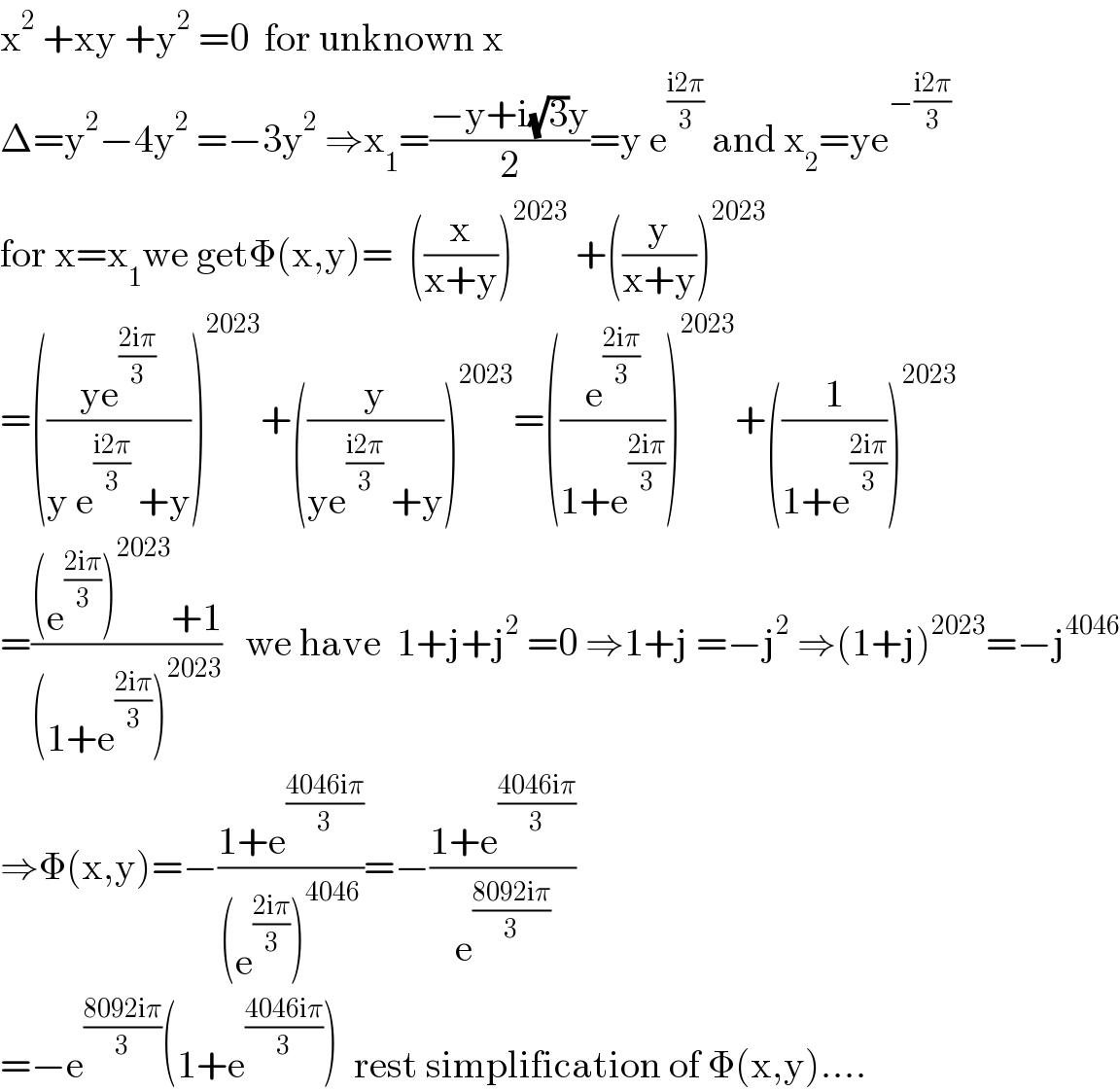
x^2 +xy +y^2 =0 for unknown x Δ=y^2 −4y^2 =−3y^2 ⇒x_1 =((−y+i(√3)y)/2)=y e^((i2π)/3) and x_2 =ye^(−((i2π)/3)) for x=x_1 we getΦ(x,y)= ((x/(x+y)))^(2023) +((y/(x+y)))^(2023) =(((ye^((2iπ)/3) )/(y e^((i2π)/3) +y)))^(2023) +((y/(ye^((i2π)/3) +y)))^(2023) =((e^((2iπ)/3) /(1+e^((2iπ)/3) )))^(2023) +((1/(1+e^((2iπ)/3) )))^(2023) =(((e^((2iπ)/3) )^(2023) +1)/((1+e^((2iπ)/3) )^(2023) )) we have 1+j+j^2 =0 ⇒1+j =−j^2 ⇒(1+j)^(2023) =−j^(4046) ⇒Φ(x,y)=−((1+e^((4046iπ)/3) )/((e^((2iπ)/3) )^(4046) ))=−((1+e^((4046iπ)/3) )/e^((8092iπ)/3) ) =−e^((8092iπ)/3) (1+e^((4046iπ)/3) ) rest simplification of Φ(x,y)....
$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{xy}\:+\mathrm{y}^{\mathrm{2}} \:=\mathrm{0}\:\:\mathrm{for}\:\mathrm{unknown}\:\mathrm{x} \\ $$$$\Delta=\mathrm{y}^{\mathrm{2}} −\mathrm{4y}^{\mathrm{2}} \:=−\mathrm{3y}^{\mathrm{2}} \:\Rightarrow\mathrm{x}_{\mathrm{1}} =\frac{−\mathrm{y}+\mathrm{i}\sqrt{\mathrm{3}}\mathrm{y}}{\mathrm{2}}=\mathrm{y}\:\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:\mathrm{and}\:\mathrm{x}_{\mathrm{2}} =\mathrm{ye}^{−\frac{\mathrm{i2}\pi}{\mathrm{3}}} \\ $$$$\mathrm{for}\:\mathrm{x}=\mathrm{x}_{\mathrm{1}} \mathrm{we}\:\mathrm{get}\Phi\left(\mathrm{x},\mathrm{y}\right)=\:\:\left(\frac{\mathrm{x}}{\mathrm{x}+\mathrm{y}}\right)^{\mathrm{2023}} \:+\left(\frac{\mathrm{y}}{\mathrm{x}+\mathrm{y}}\right)^{\mathrm{2023}} \\ $$$$=\left(\frac{\mathrm{ye}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} }{\mathrm{y}\:\mathrm{e}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:+\mathrm{y}}\right)^{\mathrm{2023}} +\left(\frac{\mathrm{y}}{\mathrm{ye}^{\frac{\mathrm{i2}\pi}{\mathrm{3}}} \:+\mathrm{y}}\right)^{\mathrm{2023}} =\left(\frac{\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} }{\mathrm{1}+\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} }\right)^{\mathrm{2023}} +\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} }\right)^{\mathrm{2023}} \\ $$$$=\frac{\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)^{\mathrm{2023}} +\mathrm{1}}{\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)^{\mathrm{2023}} }\:\:\:\mathrm{we}\:\mathrm{have}\:\:\mathrm{1}+\mathrm{j}+\mathrm{j}^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow\mathrm{1}+\mathrm{j}\:=−\mathrm{j}^{\mathrm{2}} \:\Rightarrow\left(\mathrm{1}+\mathrm{j}\right)^{\mathrm{2023}} =−\mathrm{j}^{\mathrm{4046}} \\ $$$$\Rightarrow\Phi\left(\mathrm{x},\mathrm{y}\right)=−\frac{\mathrm{1}+\mathrm{e}^{\frac{\mathrm{4046i}\pi}{\mathrm{3}}} }{\left(\mathrm{e}^{\frac{\mathrm{2i}\pi}{\mathrm{3}}} \right)^{\mathrm{4046}} }=−\frac{\mathrm{1}+\mathrm{e}^{\frac{\mathrm{4046i}\pi}{\mathrm{3}}} }{\mathrm{e}^{\frac{\mathrm{8092i}\pi}{\mathrm{3}}} } \\ $$$$=−\mathrm{e}^{\frac{\mathrm{8092i}\pi}{\mathrm{3}}} \left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{4046i}\pi}{\mathrm{3}}} \right)\:\:\mathrm{rest}\:\mathrm{simplification}\:\mathrm{of}\:\Phi\left(\mathrm{x},\mathrm{y}\right)…. \\ $$
Answered by mr W last updated on 02/May/21
let t=(y/x) x^2 +tx^2 +t^2 x^2 =0 t^2 +t+1=0 ⇒t+1=−t^2 (1/t^2 )+(1/t)+1=0 (1/t)≠1 ((1/t^2 )+(1/t)+1)((1/t)−1)=0 ((1/t))^3 −1=0 ⇒((1/t))^3 =1 ((x/(x+y)))^(2023) +((y/(x+y)))^(2023) =((1/(1+t)))^(2023) +((t/(1+t)))^(2023) =(−(1/t^2 ))^(2023) +(−(1/t))^(2023) =−((1/t^2 ))^(2023) −((1/t))^(2023) =−((1/t))^(3×1348) ((1/t))^2 −((1/t))^(3×674) ((1/t)) =−((1/t))^2 −((1/t)) =−[((1/t))^2 +((1/t))+1]+1 =−0+1 =1
$${let}\:{t}=\frac{{y}}{{x}} \\ $$$${x}^{\mathrm{2}} +{tx}^{\mathrm{2}} +{t}^{\mathrm{2}} {x}^{\mathrm{2}} =\mathrm{0} \\ $$$${t}^{\mathrm{2}} +{t}+\mathrm{1}=\mathrm{0}\:\Rightarrow{t}+\mathrm{1}=−{t}^{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{{t}}+\mathrm{1}=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{t}}\neq\mathrm{1} \\ $$$$\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{{t}}+\mathrm{1}\right)\left(\frac{\mathrm{1}}{{t}}−\mathrm{1}\right)=\mathrm{0} \\ $$$$\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{3}} =\mathrm{1} \\ $$$$ \\ $$$$\left(\frac{{x}}{{x}+{y}}\right)^{\mathrm{2023}} +\left(\frac{{y}}{{x}+{y}}\right)^{\mathrm{2023}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{1}+{t}}\right)^{\mathrm{2023}} +\left(\frac{{t}}{\mathrm{1}+{t}}\right)^{\mathrm{2023}} \\ $$$$=\left(−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)^{\mathrm{2023}} +\left(−\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2023}} \\ $$$$=−\left(\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\right)^{\mathrm{2023}} −\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2023}} \\ $$$$=−\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{3}×\mathrm{1348}} \left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{3}×\mathrm{674}} \left(\frac{\mathrm{1}}{{t}}\right) \\ $$$$=−\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{{t}}\right) \\ $$$$=−\left[\left(\frac{\mathrm{1}}{{t}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{1}}{{t}}\right)+\mathrm{1}\right]+\mathrm{1} \\ $$$$=−\mathrm{0}+\mathrm{1} \\ $$$$=\mathrm{1} \\ $$
Commented by qaz last updated on 04/May/21
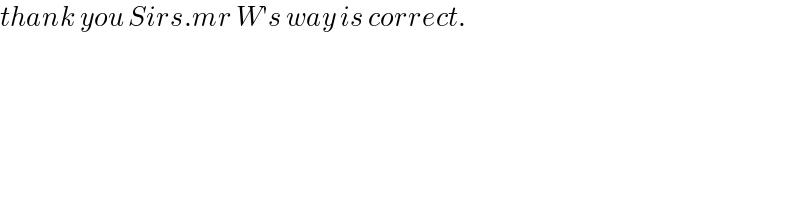
thank you Sirs.mr W′s way is correct.
$${thank}\:{you}\:{Sirs}.{mr}\:{W}'{s}\:{way}\:{is}\:{correct}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *