if-x-2-y-2-p-x-3-y-3-q-find-x-n-y-n-in-terms-of-p-q-and-n-n-4-

Question Number 75778 by mr W last updated on 16/Dec/19

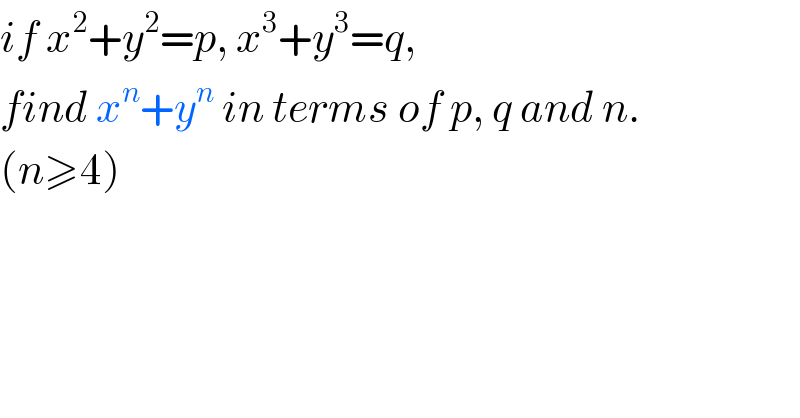
$${if}\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={p},\:{x}^{\mathrm{3}} +{y}^{\mathrm{3}} ={q}, \\ $$$${find}\:{x}^{{n}} +{y}^{{n}} \:{in}\:{terms}\:{of}\:{p},\:{q}\:{and}\:{n}. \\ $$$$\left({n}\geqslant\mathrm{4}\right) \\ $$

Answered by mind is power last updated on 17/Dec/19

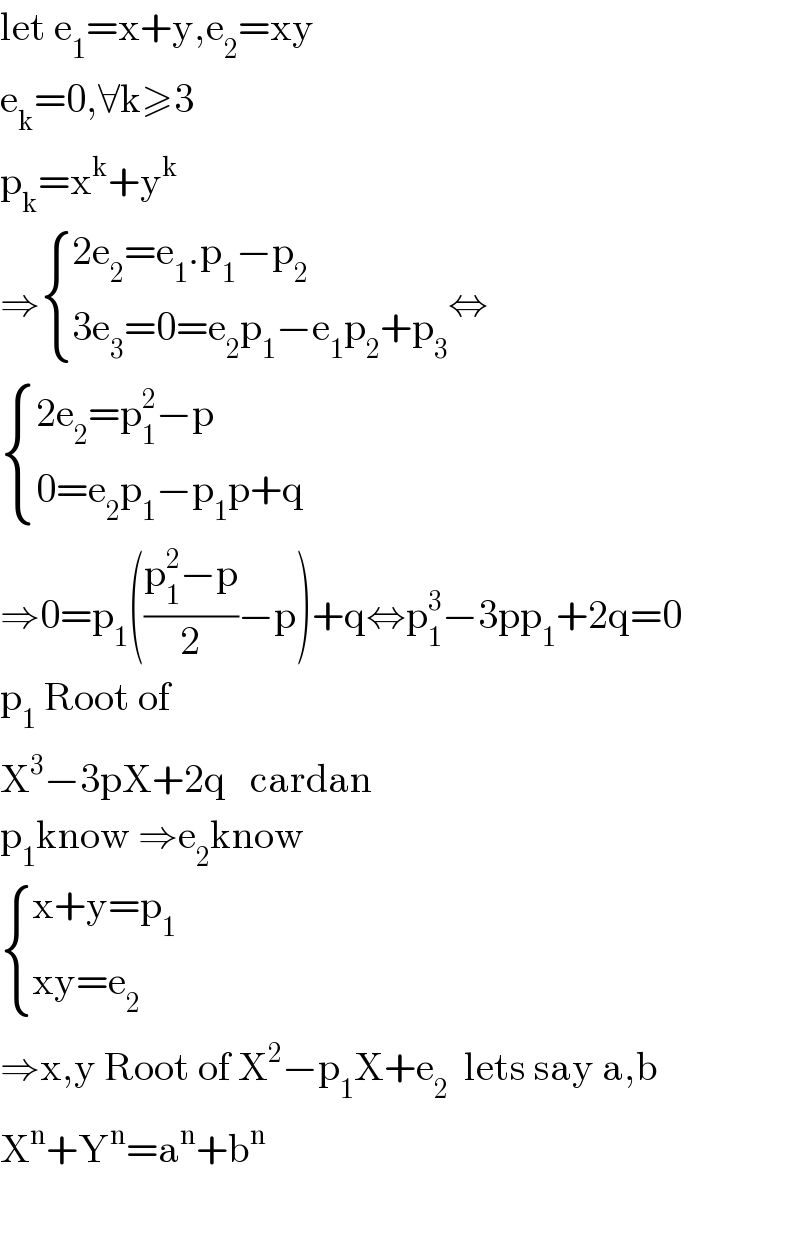
let e_1 =x+y,e_2 =xy e_k =0,∀k≥3 p_k =x^k +y^k ⇒ { ((2e_2 =e_1 .p_1 −p_2 )),((3e_3 =0=e_2 p_1 −e_1 p_2 +p_3 )) :}⇔ { ((2e_2 =p_1 ^2 −p)),((0=e_2 p_1 −p_1 p+q)) :} ⇒0=p_1 (((p_1 ^2 −p)/2)−p)+q⇔p_1 ^3 −3pp_1 +2q=0 p_1 Root of X^3 −3pX+2q cardan p_1 know ⇒e_2 know { ((x+y=p_1 )),((xy=e_2 )) :} ⇒x,y Root of X^2 −p_1 X+e_2 lets say a,b X^n +Y^n =a^n +b^n

$$\mathrm{let}\:\mathrm{e}_{\mathrm{1}} =\mathrm{x}+\mathrm{y},\mathrm{e}_{\mathrm{2}} =\mathrm{xy} \\ $$$$\mathrm{e}_{\mathrm{k}} =\mathrm{0},\forall\mathrm{k}\geqslant\mathrm{3} \\ $$$$\mathrm{p}_{\mathrm{k}} =\mathrm{x}^{\mathrm{k}} +\mathrm{y}^{\mathrm{k}} \\ $$$$\Rightarrow\begin{cases}{\mathrm{2e}_{\mathrm{2}} =\mathrm{e}_{\mathrm{1}} .\mathrm{p}_{\mathrm{1}} −\mathrm{p}_{\mathrm{2}} }\\{\mathrm{3e}_{\mathrm{3}} =\mathrm{0}=\mathrm{e}_{\mathrm{2}} \mathrm{p}_{\mathrm{1}} −\mathrm{e}_{\mathrm{1}} \mathrm{p}_{\mathrm{2}} +\mathrm{p}_{\mathrm{3}} }\end{cases}\Leftrightarrow \\ $$$$\begin{cases}{\mathrm{2e}_{\mathrm{2}} =\mathrm{p}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{p}}\\{\mathrm{0}=\mathrm{e}_{\mathrm{2}} \mathrm{p}_{\mathrm{1}} −\mathrm{p}_{\mathrm{1}} \mathrm{p}+\mathrm{q}}\end{cases} \\ $$$$\Rightarrow\mathrm{0}=\mathrm{p}_{\mathrm{1}} \left(\frac{\mathrm{p}_{\mathrm{1}} ^{\mathrm{2}} −\mathrm{p}}{\mathrm{2}}−\mathrm{p}\right)+\mathrm{q}\Leftrightarrow\mathrm{p}_{\mathrm{1}} ^{\mathrm{3}} −\mathrm{3pp}_{\mathrm{1}} +\mathrm{2q}=\mathrm{0} \\ $$$$\mathrm{p}_{\mathrm{1}} \:\mathrm{Root}\:\mathrm{of} \\ $$$$\mathrm{X}^{\mathrm{3}} −\mathrm{3pX}+\mathrm{2q}\:\:\:\mathrm{cardan} \\ $$$$\mathrm{p}_{\mathrm{1}} \mathrm{know}\:\Rightarrow\mathrm{e}_{\mathrm{2}} \mathrm{know} \\ $$$$\begin{cases}{\mathrm{x}+\mathrm{y}=\mathrm{p}_{\mathrm{1}} }\\{\mathrm{xy}=\mathrm{e}_{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow\mathrm{x},\mathrm{y}\:\mathrm{Root}\:\mathrm{of}\:\mathrm{X}^{\mathrm{2}} −\mathrm{p}_{\mathrm{1}} \mathrm{X}+\mathrm{e}_{\mathrm{2}} \:\:\mathrm{lets}\:\mathrm{say}\:\mathrm{a},\mathrm{b} \\ $$$$\mathrm{X}^{\mathrm{n}} +\mathrm{Y}^{\mathrm{n}} =\mathrm{a}^{\mathrm{n}} +\mathrm{b}^{\mathrm{n}} \\ $$$$ \\ $$

Commented by mr W last updated on 18/Dec/19

$${thank}\:{you}\:{sir}! \\ $$

Facebook Tweet Pin

if-x-2-y-2-p-x-3-y-3-q-find-x-n-y-n-in-terms-of-p-q-and-n-n-4-

Leave a Reply Cancel reply