Question Number 11701 by Nayon last updated on 30/Mar/17
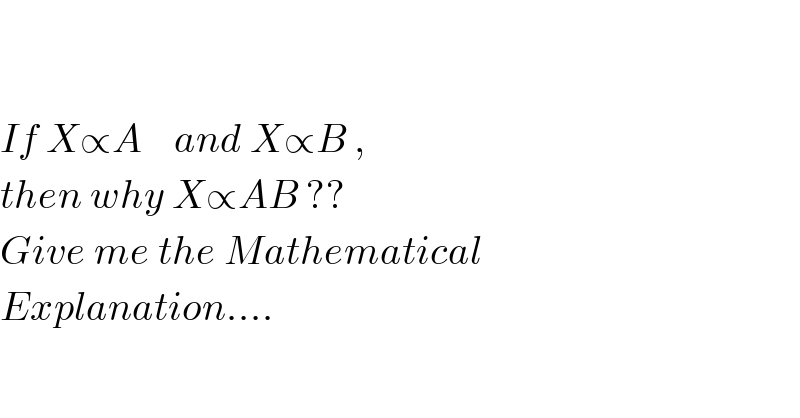
$$ \\ $$$$ \\ $$$${If}\:{X}\propto{A}\:\:\:\:{and}\:{X}\propto{B}\:, \\ $$$${then}\:{why}\:{X}\propto{AB}\:?? \\ $$$${Give}\:{me}\:{the}\:{Mathematical} \\ $$$${Explanation}…. \\ $$$$ \\ $$
Commented by Nayon last updated on 30/Mar/17

$${mrw}\mathrm{1}\:{pls}\:{solve} \\ $$
Commented by mrW1 last updated on 01/Apr/17

$${X}\propto{A}\:{means}\:{X}\:{and}\:{A}\:{are}\:{proportional}, \\ $$$${i}.{e}.\:\frac{{X}}{{A}}={k}_{\mathrm{1}} ={constant}\neq\mathrm{0} \\ $$$${but}\:{X}\:{and}\:{A}\:{are}\:{not}\:{constant}! \\ $$$$ \\ $$$${In}\:{the}\:{same}\:{way}:\:\frac{{X}}{{B}}={k}_{\mathrm{2}} ={constant}\neq\mathrm{0} \\ $$$$ \\ $$$$\frac{{X}}{{AB}}=\frac{{X}}{\frac{{X}}{{k}_{\mathrm{1}} }×\frac{{X}}{{k}_{\mathrm{2}} }}=\frac{{k}_{\mathrm{1}} {k}_{\mathrm{2}} }{{X}}=\frac{{constant}}{{no}\:{constant}}\neq{constant} \\ $$$$\Rightarrow{X}\:{and}\:{AB}\:{are}\:{not}\:{proportional}! \\ $$$${i}.{e}.\:{X}\propto{AB}\:{is}\:{not}\:{true}! \\ $$$$ \\ $$$${Example}: \\ $$$${A}=\mathrm{2}{X} \\ $$$${B}=\mathrm{3}{X} \\ $$$$\frac{{X}}{{A}}=\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow{X}\propto{A} \\ $$$$\frac{{X}}{{B}}=\frac{\mathrm{1}}{\mathrm{3}}\Rightarrow{X}\propto{B} \\ $$$${but} \\ $$$$\frac{{X}}{{AB}}=\frac{{X}}{\mathrm{6}{X}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{6}{X}}\neq{constant} \\ $$$$\Rightarrow{X}\:{not}\:\propto{AB}! \\ $$
Commented by Nayon last updated on 03/Apr/17
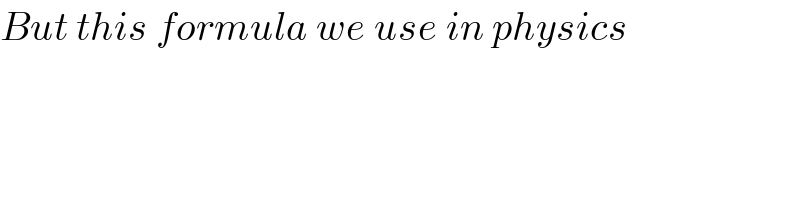
$${But}\:{this}\:{formula}\:{we}\:{use}\:{in}\:{physics} \\ $$
Answered by linkelly0615 last updated on 30/Mar/17
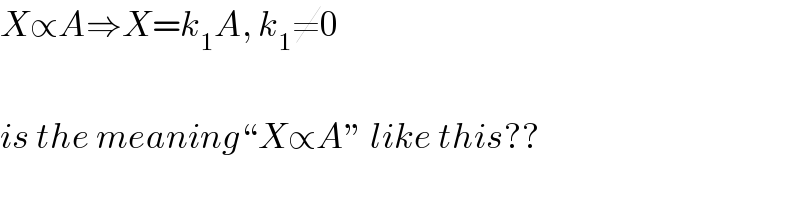
$${X}\propto{A}\Rightarrow{X}={k}_{\mathrm{1}} {A},\:{k}_{\mathrm{1}} \neq\mathrm{0} \\ $$$$ \\ $$$${is}\:{the}\:{meaning}“{X}\propto{A}''\:{like}\:{this}?? \\ $$
Commented by linkelly0615 last updated on 30/Mar/17

$$ \\ $$$$ \\ $$$${If}\:{my}\:{view}\:{is}\:{right}… \\ $$$${then}\:{it}\:{should}\:{be}\:{written}\:{as}“{X}^{\mathrm{2}} \propto{AB}''. \\ $$
Commented by Nayon last updated on 30/Mar/17

$${no}\:,\:{it}\:{is}\:{X}\propto{AB} \\ $$
Commented by Nayon last updated on 30/Mar/17
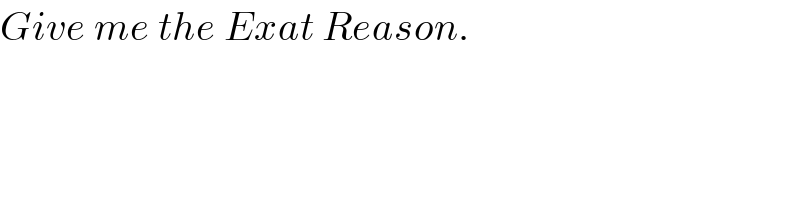
$${Give}\:{me}\:{the}\:{Exat}\:{Reason}. \\ $$
Answered by linkelly0615 last updated on 30/Mar/17
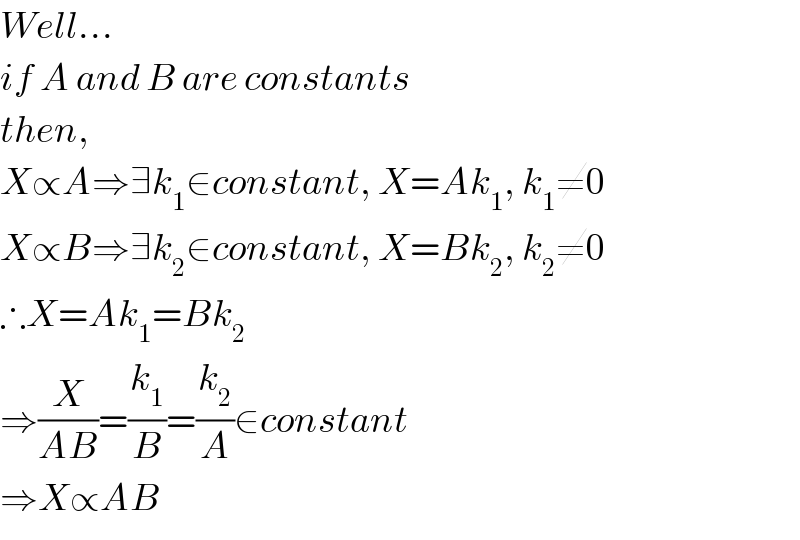
$${Well}… \\ $$$${if}\:{A}\:{and}\:{B}\:{are}\:{constants} \\ $$$${then}, \\ $$$${X}\propto{A}\Rightarrow\exists{k}_{\mathrm{1}} \in{constant},\:{X}={Ak}_{\mathrm{1}} ,\:{k}_{\mathrm{1}} \neq\mathrm{0} \\ $$$${X}\propto{B}\Rightarrow\exists{k}_{\mathrm{2}} \in{constant},\:{X}={Bk}_{\mathrm{2}} ,\:{k}_{\mathrm{2}} \neq\mathrm{0} \\ $$$$\therefore{X}={Ak}_{\mathrm{1}} ={Bk}_{\mathrm{2}} \\ $$$$\Rightarrow\frac{{X}}{{AB}}=\frac{{k}_{\mathrm{1}} }{{B}}=\frac{{k}_{\mathrm{2}} }{{A}}\in{constant} \\ $$$$\Rightarrow{X}\propto{AB} \\ $$
