Question Number 133612 by benjo_mathlover last updated on 23/Feb/21
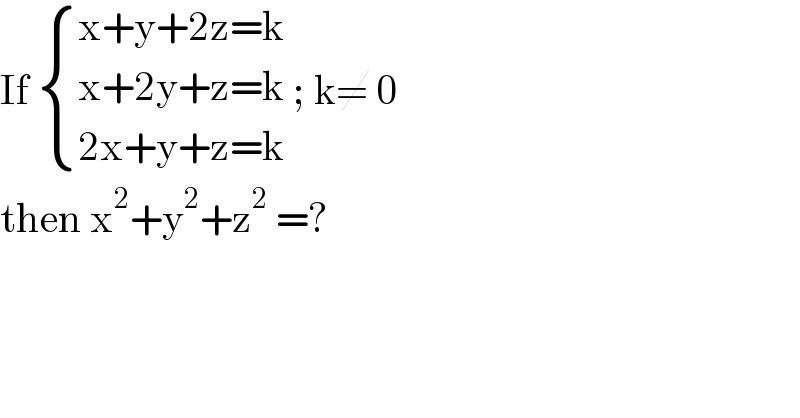
$$\mathrm{If}\:\begin{cases}{\mathrm{x}+\mathrm{y}+\mathrm{2z}=\mathrm{k}}\\{\mathrm{x}+\mathrm{2y}+\mathrm{z}=\mathrm{k}}\\{\mathrm{2x}+\mathrm{y}+\mathrm{z}=\mathrm{k}}\end{cases}\:;\:\mathrm{k}\neq\:\mathrm{0} \\ $$$$\mathrm{then}\:\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \:=? \\ $$$$ \\ $$
Commented by mr W last updated on 23/Feb/21

$${x}={y}={z}=\frac{{k}}{\mathrm{4}} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} =\frac{\mathrm{3}{k}^{\mathrm{2}} }{\mathrm{16}} \\ $$
Commented by mr W last updated on 23/Feb/21
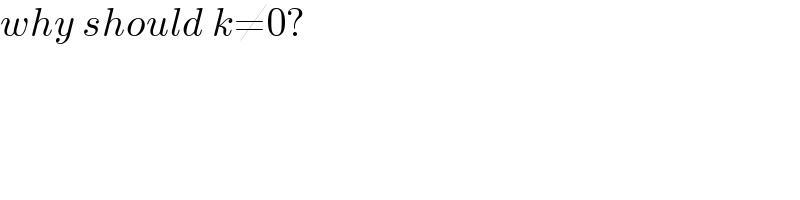
$${why}\:{should}\:{k}\neq\mathrm{0}? \\ $$
