if-x-y-and-z-are-solution-of-x-xy-x-y-1-2-2x-xz-x-z-2-3-2-2y-z-yz-y-z-3-4-so-the-value-of-1-x-1-y-1-1-z-2-

Question Number 11764 by Peter last updated on 31/Mar/17

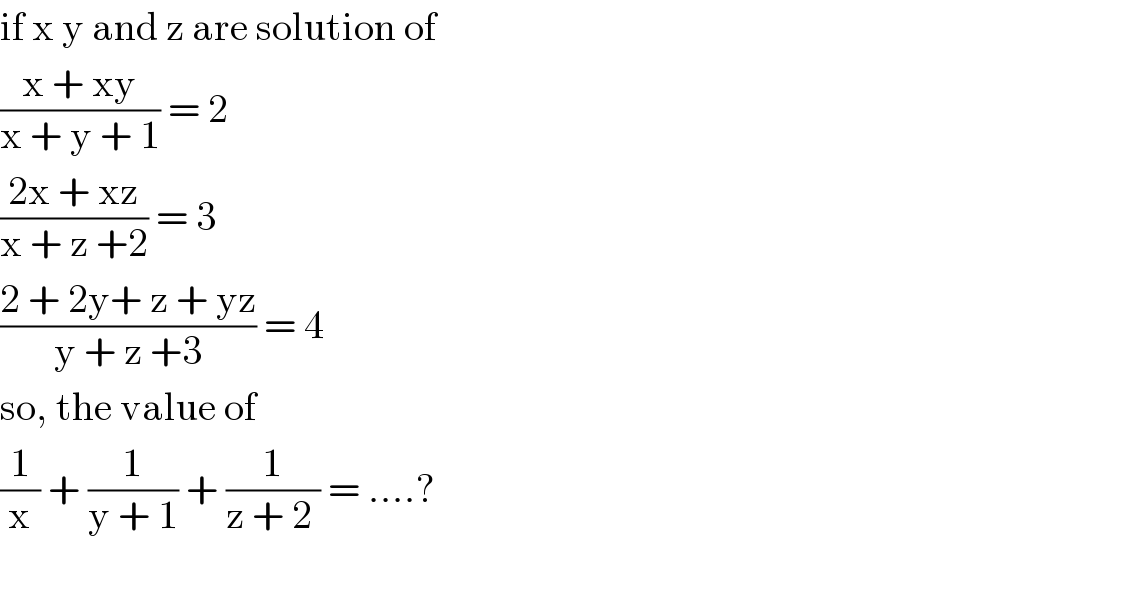
$$\mathrm{if}\:\mathrm{x}\:\mathrm{y}\:\mathrm{and}\:\mathrm{z}\:\mathrm{are}\:\mathrm{solution}\:\mathrm{of} \\ $$$$\frac{\mathrm{x}\:+\:\mathrm{xy}}{\mathrm{x}\:+\:\mathrm{y}\:+\:\mathrm{1}}\:=\:\mathrm{2} \\ $$$$\frac{\mathrm{2x}\:+\:\mathrm{xz}}{\mathrm{x}\:+\:\mathrm{z}\:+\mathrm{2}}\:=\:\mathrm{3} \\ $$$$\frac{\mathrm{2}\:+\:\mathrm{2y}+\:\mathrm{z}\:+\:\mathrm{yz}}{\mathrm{y}\:+\:\mathrm{z}\:+\mathrm{3}}\:=\:\mathrm{4} \\ $$$$\mathrm{so},\:\mathrm{the}\:\mathrm{value}\:\mathrm{of} \\ $$$$\frac{\mathrm{1}}{\mathrm{x}}\:+\:\frac{\mathrm{1}}{\mathrm{y}\:+\:\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{z}\:+\:\mathrm{2}\:}\:=\:….? \\ $$$$ \\ $$

Answered by ajfour last updated on 31/Mar/17

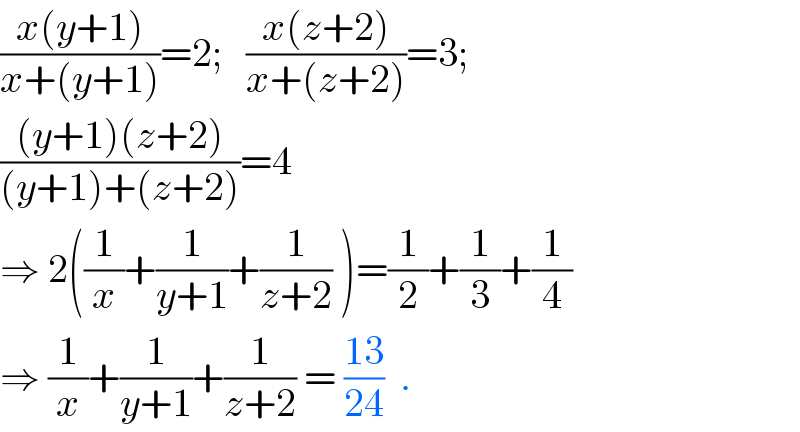
((x(y+1))/(x+(y+1)))=2; ((x(z+2))/(x+(z+2)))=3; (((y+1)(z+2))/((y+1)+(z+2)))=4 ⇒ 2((1/x)+(1/(y+1))+(1/(z+2)) )=(1/2)+(1/3)+(1/4) ⇒ (1/x)+(1/(y+1))+(1/(z+2)) = ((13)/(24)) .

$$\frac{{x}\left({y}+\mathrm{1}\right)}{{x}+\left({y}+\mathrm{1}\right)}=\mathrm{2};\:\:\:\frac{{x}\left({z}+\mathrm{2}\right)}{{x}+\left({z}+\mathrm{2}\right)}=\mathrm{3}; \\ $$$$\frac{\left({y}+\mathrm{1}\right)\left({z}+\mathrm{2}\right)}{\left({y}+\mathrm{1}\right)+\left({z}+\mathrm{2}\right)}=\mathrm{4} \\ $$$$\Rightarrow\:\mathrm{2}\left(\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}+\mathrm{1}}+\frac{\mathrm{1}}{{z}+\mathrm{2}}\:\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{y}+\mathrm{1}}+\frac{\mathrm{1}}{{z}+\mathrm{2}}\:=\:\frac{\mathrm{13}}{\mathrm{24}}\:\:. \\ $$

Facebook Tweet Pin

if-x-y-and-z-are-solution-of-x-xy-x-y-1-2-2x-xz-x-z-2-3-2-2y-z-yz-y-z-3-4-so-the-value-of-1-x-1-y-1-1-z-2-

Leave a Reply Cancel reply