Question Number 5903 by sanusihammed last updated on 04/Jun/16
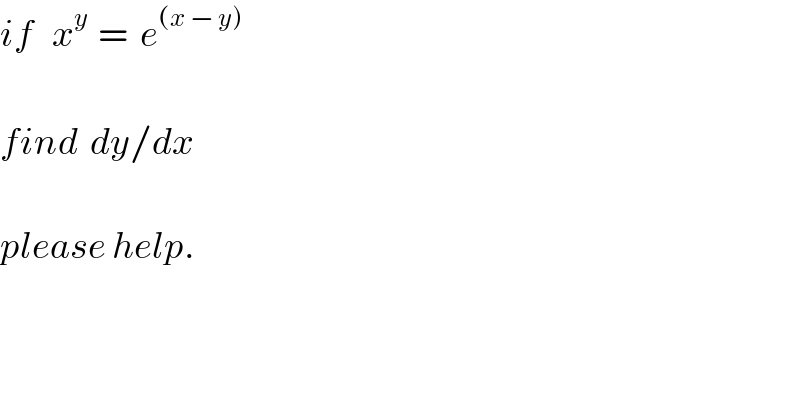
$${if}\:\:\:{x}^{{y}\:} \:=\:\:{e}^{\left({x}\:−\:{y}\right)} \\ $$$$ \\ $$$${find}\:\:{dy}/{dx} \\ $$$$ \\ $$$${please}\:{help}. \\ $$
Answered by uchechukwu okorie favour last updated on 10/Aug/16
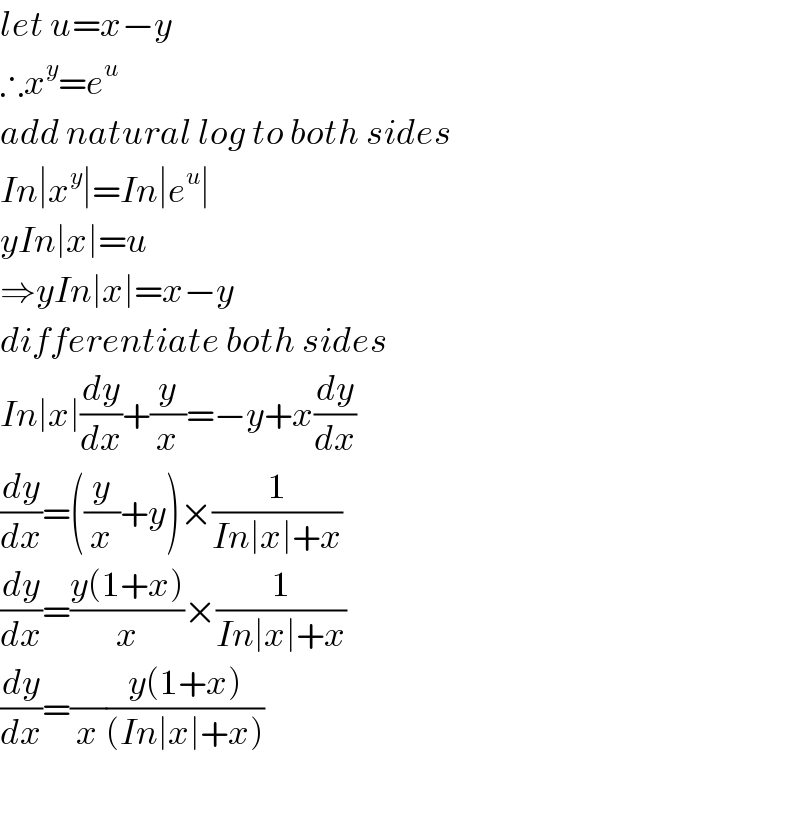
$${let}\:{u}={x}−{y} \\ $$$$\therefore{x}^{{y}} ={e}^{{u}} \\ $$$${add}\:{natural}\:{log}\:{to}\:{both}\:{sides} \\ $$$${In}\mid{x}^{{y}} \mid={In}\mid{e}^{{u}} \mid \\ $$$${yIn}\mid{x}\mid={u} \\ $$$$\Rightarrow{yIn}\mid{x}\mid={x}−{y} \\ $$$${differentiate}\:{both}\:{sides} \\ $$$${In}\mid{x}\mid\frac{{dy}}{{dx}}+\frac{{y}}{{x}}=−{y}+{x}\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}=\left(\frac{{y}}{{x}}+{y}\right)×\frac{\mathrm{1}}{{In}\mid{x}\mid+{x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{{y}\left(\mathrm{1}+{x}\right)}{{x}}×\frac{\mathrm{1}}{{In}\mid{x}\mid+{x}} \\ $$$$\frac{{dy}}{{dx}}=\frac{}{{x}}\frac{{y}\left(\mathrm{1}+{x}\right)}{\left({In}\mid{x}\mid+{x}\right)} \\ $$$$ \\ $$
