Menu Close

if-x-y-z-gt-0-prove-that-x-z-2-e-z-x-2-y-x-2-e-x-y-2-z-y-2-e-y-z-2-3e-

Tinku Tara 0 Comments
Pin




Question Number 143410 by mathdanisur last updated on 14/Jun/21
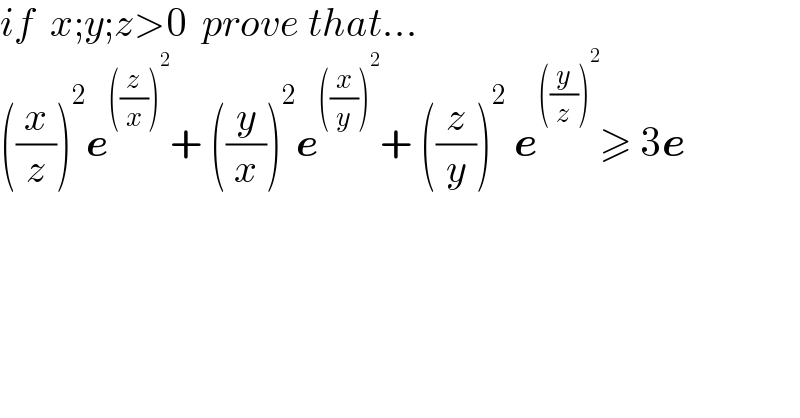
if x;y;z>0 prove that... ((x/z))^2 e^(((z/x))^2 ) + ((y/x))^2 e^(((x/y))^2 ) + ((z/y))^2 e^(((y/z))^2 ) ≥ 3e
$${if}\:\:{x};{y};{z}>\mathrm{0}\:\:{prove}\:{that}… \\ $$$$\left(\frac{{x}}{{z}}\right)^{\mathrm{2}} \boldsymbol{{e}}^{\left(\frac{{z}}{{x}}\right)^{\mathrm{2}} } +\:\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \boldsymbol{{e}}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } +\:\left(\frac{{z}}{{y}}\right)^{\mathrm{2}} \:\boldsymbol{{e}}^{\left(\frac{{y}}{{z}}\right)^{\mathrm{2}} } \geqslant\:\mathrm{3}\boldsymbol{{e}} \\ $$
Commented by mr W last updated on 14/Jun/21
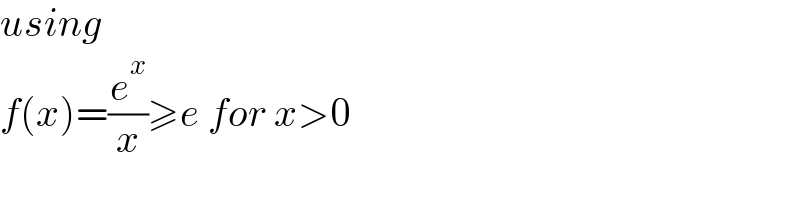
using f(x)=(e^x /x)≥e for x>0
$${using} \\ $$$${f}\left({x}\right)=\frac{{e}^{{x}} }{{x}}\geqslant{e}\:{for}\:{x}>\mathrm{0} \\ $$
Commented by mathdanisur last updated on 14/Jun/21
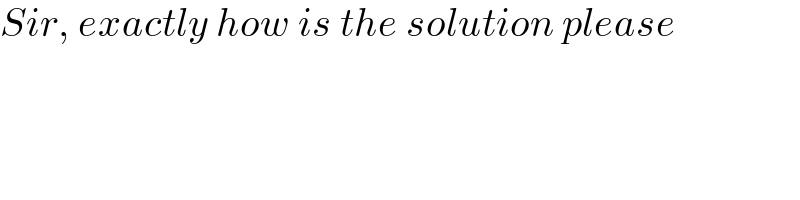
Sir, exactly how is the solution please
$${Sir},\:{exactly}\:{how}\:{is}\:{the}\:{solution}\:{please} \\ $$
Commented by mr W last updated on 14/Jun/21
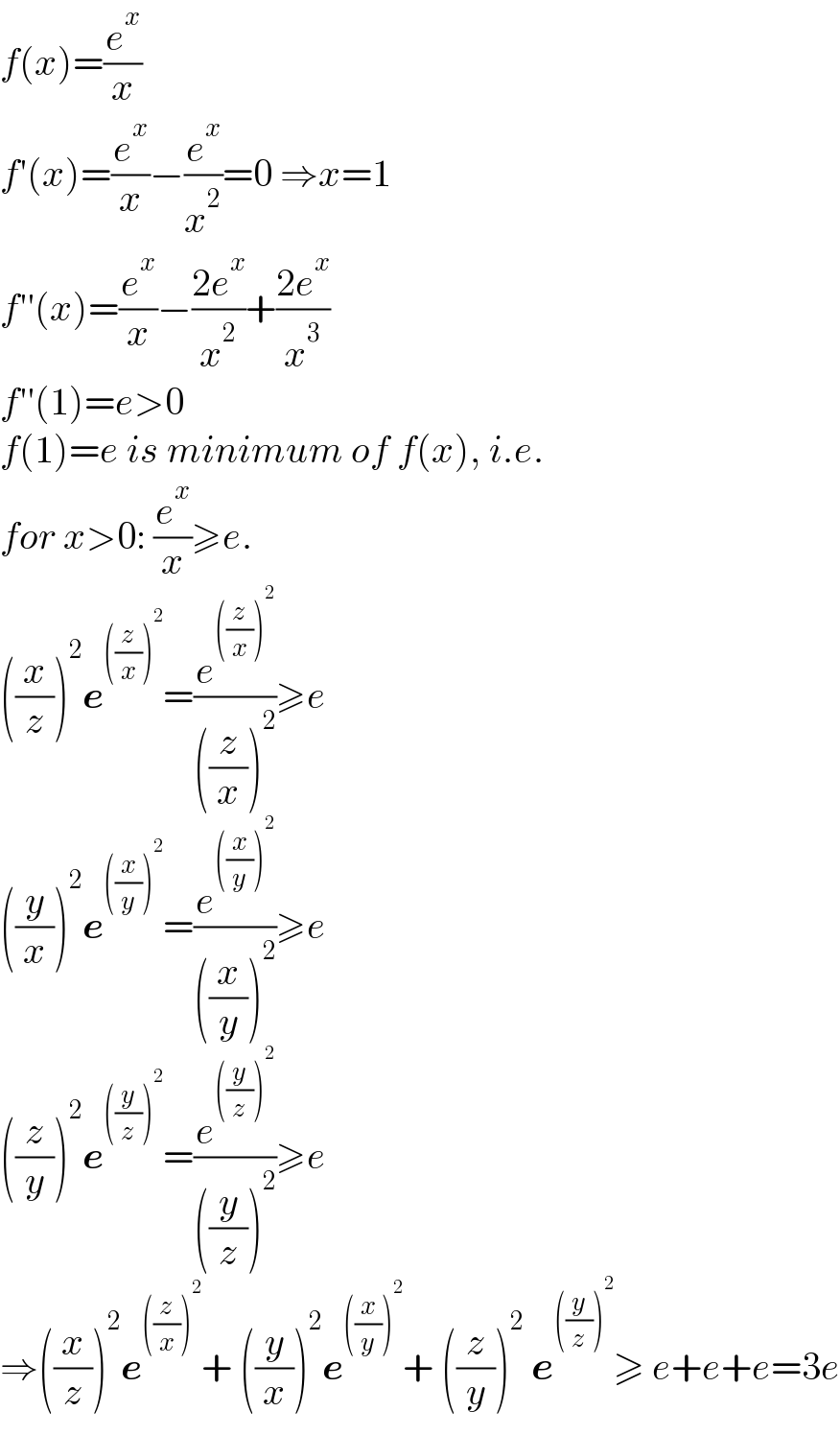
f(x)=(e^x /x) f′(x)=(e^x /x)−(e^x /x^2 )=0 ⇒x=1 f′′(x)=(e^x /x)−((2e^x )/x^2 )+((2e^x )/x^3 ) f′′(1)=e>0 f(1)=e is minimum of f(x), i.e. for x>0: (e^x /x)≥e. ((x/z))^2 e^(((z/x))^2 ) =(e^(((z/x))^2 ) /(((z/x))^2 ))≥e ((y/x))^2 e^(((x/y))^2 ) =(e^(((x/y))^2 ) /(((x/y))^2 ))≥e ((z/y))^2 e^(((y/z))^2 ) =(e^(((y/z))^2 ) /(((y/z))^2 ))≥e ⇒((x/z))^2 e^(((z/x))^2 ) + ((y/x))^2 e^(((x/y))^2 ) + ((z/y))^2 e^(((y/z))^2 ) ≥ e+e+e=3e
$${f}\left({x}\right)=\frac{{e}^{{x}} }{{x}} \\ $$$${f}'\left({x}\right)=\frac{{e}^{{x}} }{{x}}−\frac{{e}^{{x}} }{{x}^{\mathrm{2}} }=\mathrm{0}\:\Rightarrow{x}=\mathrm{1} \\ $$$${f}''\left({x}\right)=\frac{{e}^{{x}} }{{x}}−\frac{\mathrm{2}{e}^{{x}} }{{x}^{\mathrm{2}} }+\frac{\mathrm{2}{e}^{{x}} }{{x}^{\mathrm{3}} } \\ $$$${f}''\left(\mathrm{1}\right)={e}>\mathrm{0} \\ $$$${f}\left(\mathrm{1}\right)={e}\:{is}\:{minimum}\:{of}\:{f}\left({x}\right),\:{i}.{e}. \\ $$$${for}\:{x}>\mathrm{0}:\:\frac{{e}^{{x}} }{{x}}\geqslant{e}. \\ $$$$\left(\frac{{x}}{{z}}\right)^{\mathrm{2}} \boldsymbol{{e}}^{\left(\frac{{z}}{{x}}\right)^{\mathrm{2}} } =\frac{{e}^{\left(\frac{{z}}{{x}}\right)^{\mathrm{2}} } }{\left(\frac{{z}}{{x}}\right)^{\mathrm{2}} }\geqslant{e} \\ $$$$\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \boldsymbol{{e}}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } =\frac{{e}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } }{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} }\geqslant{e} \\ $$$$\left(\frac{{z}}{{y}}\right)^{\mathrm{2}} \boldsymbol{{e}}^{\left(\frac{{y}}{{z}}\right)^{\mathrm{2}} } =\frac{{e}^{\left(\frac{{y}}{{z}}\right)^{\mathrm{2}} } }{\left(\frac{{y}}{{z}}\right)^{\mathrm{2}} }\geqslant{e} \\ $$$$\Rightarrow\left(\frac{{x}}{{z}}\right)^{\mathrm{2}} \boldsymbol{{e}}^{\left(\frac{{z}}{{x}}\right)^{\mathrm{2}} } +\:\left(\frac{{y}}{{x}}\right)^{\mathrm{2}} \boldsymbol{{e}}^{\left(\frac{{x}}{{y}}\right)^{\mathrm{2}} } +\:\left(\frac{{z}}{{y}}\right)^{\mathrm{2}} \:\boldsymbol{{e}}^{\left(\frac{{y}}{{z}}\right)^{\mathrm{2}} } \geqslant\:{e}+{e}+{e}=\mathrm{3}{e} \\ $$
Commented by mathdanisur last updated on 14/Jun/21
cool Sir thank you
$${cool}\:{Sir}\:{thank}\:{you} \\ $$
Answered by SEIJacob last updated on 14/Jun/21
$$ \\ $$$$ \\ $$
Answered by mindispower last updated on 14/Jun/21
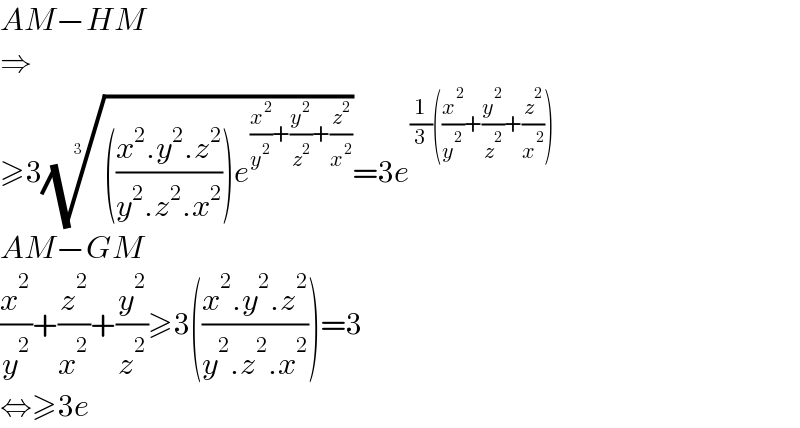
AM−HM ⇒ ≥3(((((x^2 .y^2 .z^2 )/(y^2 .z^2 .x^2 )))e^((x^2 /y^2 )+(y^2 /z^2 )+(z^2 /x^2 )) ))^(1/3) =3e^((1/3)((x^2 /y^2 )+(y^2 /z^2 )+(z^2 /x^2 ))) AM−GM (x^2 /y^2 )+(z^2 /x^2 )+(y^2 /z^2 )≥3(((x^2 .y^2 .z^2 )/(y^2 .z^2 .x^2 )))=3 ⇔≥3e
$${AM}−{HM} \\ $$$$\Rightarrow \\ $$$$\geqslant\mathrm{3}\sqrt[{\mathrm{3}}]{\left(\frac{{x}^{\mathrm{2}} .{y}^{\mathrm{2}} .{z}^{\mathrm{2}} }{{y}^{\mathrm{2}} .{z}^{\mathrm{2}} .{x}^{\mathrm{2}} }\right){e}^{\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{z}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} }} }=\mathrm{3}{e}^{\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{z}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\right)} \\ $$$${AM}−{GM} \\ $$$$\frac{{x}^{\mathrm{2}} }{{y}^{\mathrm{2}} }+\frac{{z}^{\mathrm{2}} }{{x}^{\mathrm{2}} }+\frac{{y}^{\mathrm{2}} }{{z}^{\mathrm{2}} }\geqslant\mathrm{3}\left(\frac{{x}^{\mathrm{2}} .{y}^{\mathrm{2}} .{z}^{\mathrm{2}} }{{y}^{\mathrm{2}} .{z}^{\mathrm{2}} .{x}^{\mathrm{2}} }\right)=\mathrm{3} \\ $$$$\Leftrightarrow\geqslant\mathrm{3}{e} \\ $$
Commented by mathdanisur last updated on 14/Jun/21
thanks Sir cool
$${thanks}\:{Sir}\:{cool} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *