Menu Close

If-y-2-3uy-5u-2-2-2t-2-2tu-3u-2-1-0-and-5x-2-4xt-t-2-0-find-dy-dx-and-du-dt-

Tinku Tara 0 Comments
Pin




Question Number 4487 by Rasheed Soomro last updated on 31/Jan/16
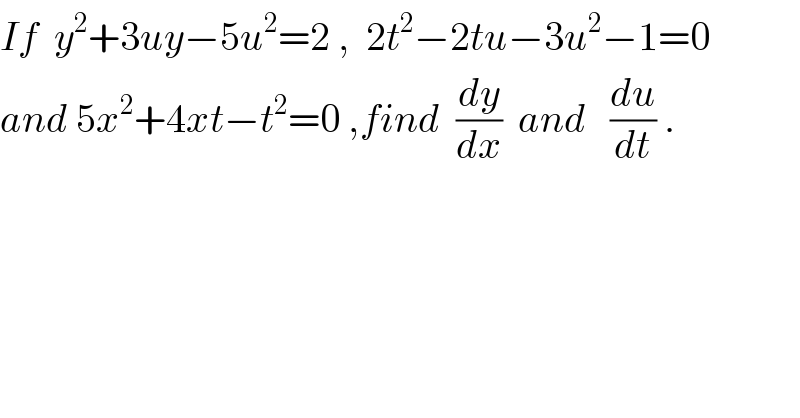
If y^2 +3uy−5u^2 =2 , 2t^2 −2tu−3u^2 −1=0 and 5x^2 +4xt−t^2 =0 ,find (dy/dx) and (du/dt) .
$${If}\:\:{y}^{\mathrm{2}} +\mathrm{3}{uy}−\mathrm{5}{u}^{\mathrm{2}} =\mathrm{2}\:,\:\:\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{tu}−\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\: \\ $$$${and}\:\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{xt}−{t}^{\mathrm{2}} =\mathrm{0}\:,{find}\:\:\frac{{dy}}{{dx}}\:\:{and}\:\:\:\frac{{du}}{{dt}}\:. \\ $$
Answered by Yozzii last updated on 31/Jan/16
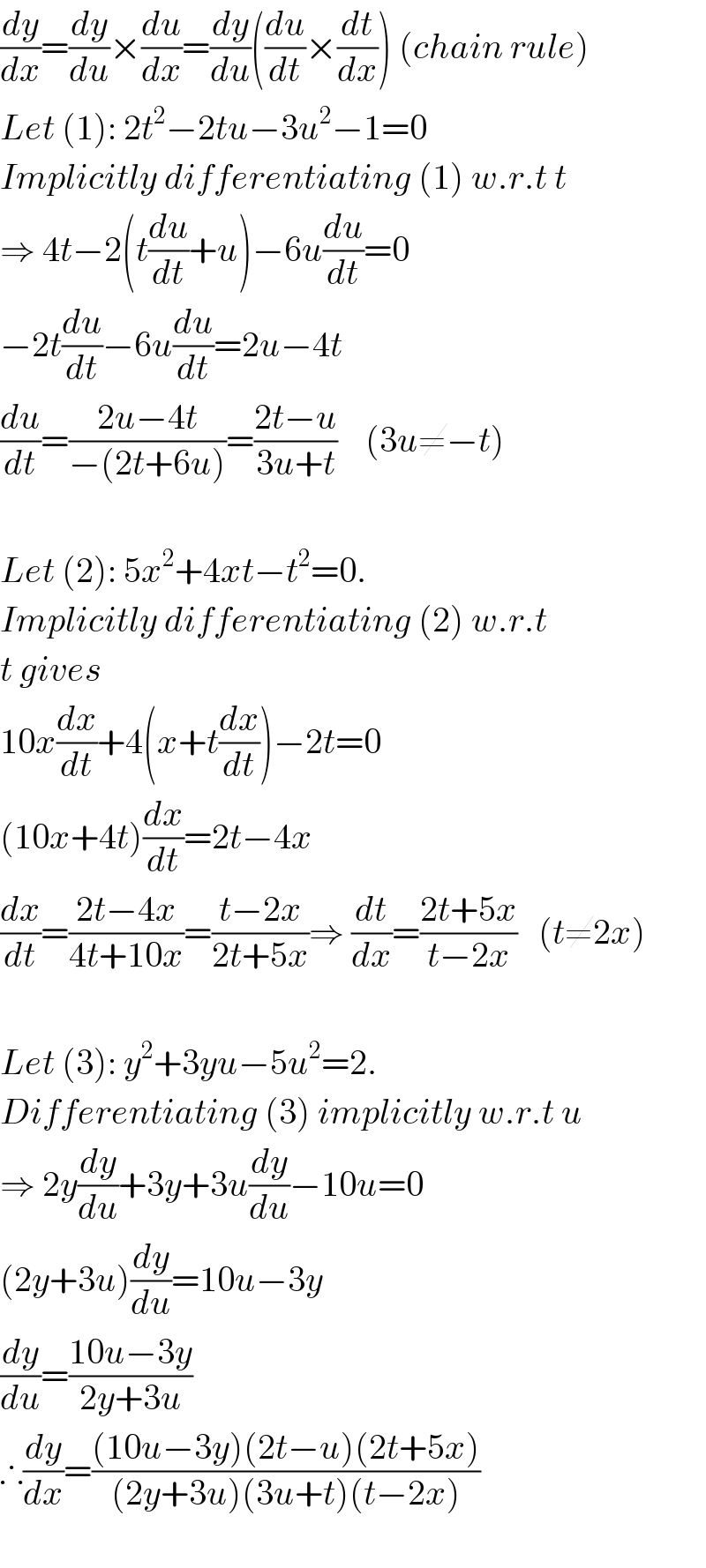
(dy/dx)=(dy/du)×(du/dx)=(dy/du)((du/dt)×(dt/dx)) (chain rule) Let (1): 2t^2 −2tu−3u^2 −1=0 Implicitly differentiating (1) w.r.t t ⇒ 4t−2(t(du/dt)+u)−6u(du/dt)=0 −2t(du/dt)−6u(du/dt)=2u−4t (du/dt)=((2u−4t)/(−(2t+6u)))=((2t−u)/(3u+t)) (3u≠−t) Let (2): 5x^2 +4xt−t^2 =0. Implicitly differentiating (2) w.r.t t gives 10x(dx/dt)+4(x+t(dx/dt))−2t=0 (10x+4t)(dx/dt)=2t−4x (dx/dt)=((2t−4x)/(4t+10x))=((t−2x)/(2t+5x))⇒ (dt/dx)=((2t+5x)/(t−2x)) (t≠2x) Let (3): y^2 +3yu−5u^2 =2. Differentiating (3) implicitly w.r.t u ⇒ 2y(dy/du)+3y+3u(dy/du)−10u=0 (2y+3u)(dy/du)=10u−3y (dy/du)=((10u−3y)/(2y+3u)) ∴(dy/dx)=(((10u−3y)(2t−u)(2t+5x))/((2y+3u)(3u+t)(t−2x)))
$$\frac{{dy}}{{dx}}=\frac{{dy}}{{du}}×\frac{{du}}{{dx}}=\frac{{dy}}{{du}}\left(\frac{{du}}{{dt}}×\frac{{dt}}{{dx}}\right)\:\left({chain}\:{rule}\right) \\ $$$${Let}\:\left(\mathrm{1}\right):\:\mathrm{2}{t}^{\mathrm{2}} −\mathrm{2}{tu}−\mathrm{3}{u}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\: \\ $$$${Implicitly}\:{differentiating}\:\left(\mathrm{1}\right)\:{w}.{r}.{t}\:{t} \\ $$$$\Rightarrow\:\mathrm{4}{t}−\mathrm{2}\left({t}\frac{{du}}{{dt}}+{u}\right)−\mathrm{6}{u}\frac{{du}}{{dt}}=\mathrm{0} \\ $$$$−\mathrm{2}{t}\frac{{du}}{{dt}}−\mathrm{6}{u}\frac{{du}}{{dt}}=\mathrm{2}{u}−\mathrm{4}{t} \\ $$$$\frac{{du}}{{dt}}=\frac{\mathrm{2}{u}−\mathrm{4}{t}}{−\left(\mathrm{2}{t}+\mathrm{6}{u}\right)}=\frac{\mathrm{2}{t}−{u}}{\mathrm{3}{u}+{t}}\:\:\:\:\left(\mathrm{3}{u}\neq−{t}\right) \\ $$$$ \\ $$$${Let}\:\left(\mathrm{2}\right):\:\mathrm{5}{x}^{\mathrm{2}} +\mathrm{4}{xt}−{t}^{\mathrm{2}} =\mathrm{0}. \\ $$$${Implicitly}\:{differentiating}\:\left(\mathrm{2}\right)\:{w}.{r}.{t} \\ $$$${t}\:{gives}\: \\ $$$$\mathrm{10}{x}\frac{{dx}}{{dt}}+\mathrm{4}\left({x}+{t}\frac{{dx}}{{dt}}\right)−\mathrm{2}{t}=\mathrm{0} \\ $$$$\left(\mathrm{10}{x}+\mathrm{4}{t}\right)\frac{{dx}}{{dt}}=\mathrm{2}{t}−\mathrm{4}{x} \\ $$$$\frac{{dx}}{{dt}}=\frac{\mathrm{2}{t}−\mathrm{4}{x}}{\mathrm{4}{t}+\mathrm{10}{x}}=\frac{{t}−\mathrm{2}{x}}{\mathrm{2}{t}+\mathrm{5}{x}}\Rightarrow\:\frac{{dt}}{{dx}}=\frac{\mathrm{2}{t}+\mathrm{5}{x}}{{t}−\mathrm{2}{x}}\:\:\:\left({t}\neq\mathrm{2}{x}\right) \\ $$$$ \\ $$$${Let}\:\left(\mathrm{3}\right):\:{y}^{\mathrm{2}} +\mathrm{3}{yu}−\mathrm{5}{u}^{\mathrm{2}} =\mathrm{2}. \\ $$$${Differentiating}\:\left(\mathrm{3}\right)\:{implicitly}\:{w}.{r}.{t}\:{u} \\ $$$$\Rightarrow\:\mathrm{2}{y}\frac{{dy}}{{du}}+\mathrm{3}{y}+\mathrm{3}{u}\frac{{dy}}{{du}}−\mathrm{10}{u}=\mathrm{0} \\ $$$$\left(\mathrm{2}{y}+\mathrm{3}{u}\right)\frac{{dy}}{{du}}=\mathrm{10}{u}−\mathrm{3}{y} \\ $$$$\frac{{dy}}{{du}}=\frac{\mathrm{10}{u}−\mathrm{3}{y}}{\mathrm{2}{y}+\mathrm{3}{u}} \\ $$$$\therefore\frac{{dy}}{{dx}}=\frac{\left(\mathrm{10}{u}−\mathrm{3}{y}\right)\left(\mathrm{2}{t}−{u}\right)\left(\mathrm{2}{t}+\mathrm{5}{x}\right)}{\left(\mathrm{2}{y}+\mathrm{3}{u}\right)\left(\mathrm{3}{u}+{t}\right)\left({t}−\mathrm{2}{x}\right)} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *