Question Number 5208 by sanusihammed last updated on 30/Apr/16

$${If}\:{y}\:=\:{x}!\: \\ $$$$ \\ $$$${Find}\:\frac{{dy}}{{dx}} \\ $$
Commented by FilupSmith last updated on 30/Apr/16
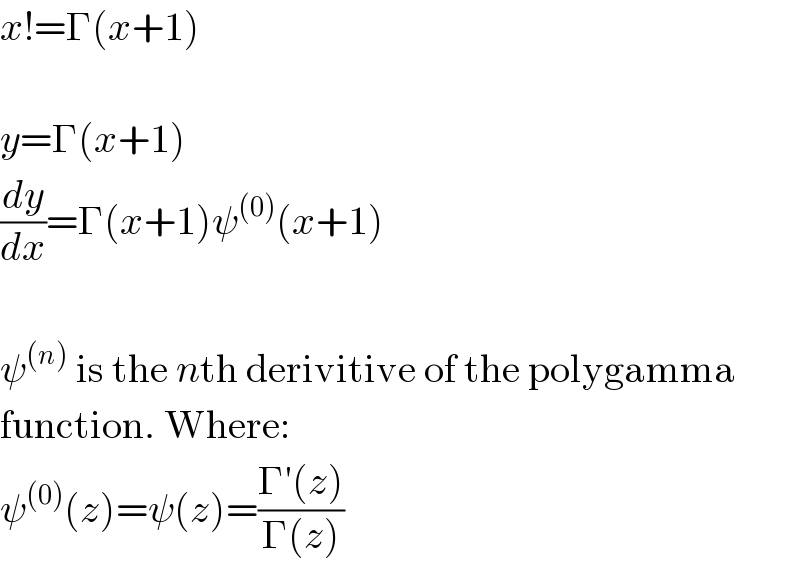
$${x}!=\Gamma\left({x}+\mathrm{1}\right) \\ $$$$ \\ $$$${y}=\Gamma\left({x}+\mathrm{1}\right) \\ $$$$\frac{{dy}}{{dx}}=\Gamma\left({x}+\mathrm{1}\right)\psi^{\left(\mathrm{0}\right)} \left({x}+\mathrm{1}\right) \\ $$$$ \\ $$$$\psi^{\left({n}\right)} \:\mathrm{is}\:\mathrm{the}\:{n}\mathrm{th}\:\mathrm{derivitive}\:\mathrm{of}\:\mathrm{the}\:\mathrm{polygamma} \\ $$$$\mathrm{function}.\:\mathrm{Where}: \\ $$$$\psi^{\left(\mathrm{0}\right)} \left({z}\right)=\psi\left({z}\right)=\frac{\Gamma'\left({z}\right)}{\Gamma\left({z}\right)} \\ $$
