Question Number 10712 by Saham last updated on 23/Feb/17
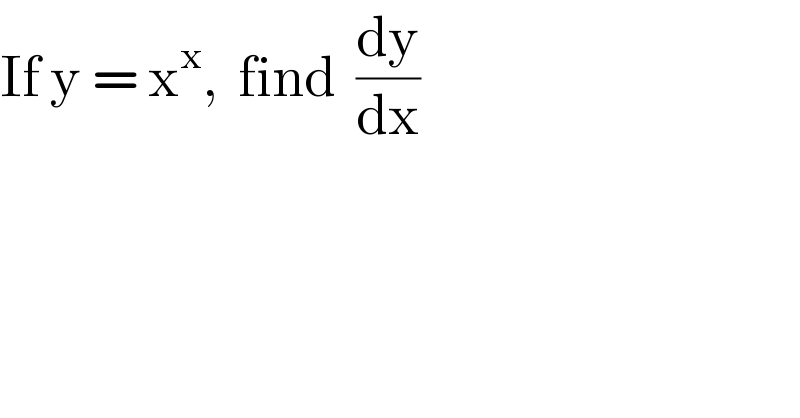
$$\mathrm{If}\:\mathrm{y}\:=\:\mathrm{x}^{\mathrm{x}} ,\:\:\mathrm{find}\:\:\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$
Answered by mrW1 last updated on 23/Feb/17
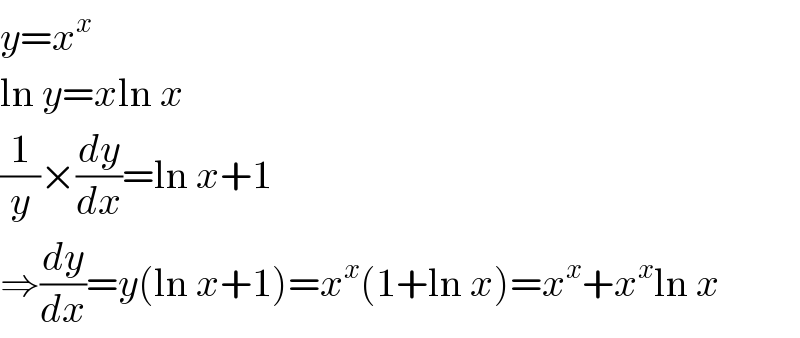
$${y}={x}^{{x}} \\ $$$$\mathrm{ln}\:{y}={x}\mathrm{ln}\:{x} \\ $$$$\frac{\mathrm{1}}{{y}}×\frac{{dy}}{{dx}}=\mathrm{ln}\:{x}+\mathrm{1} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}={y}\left(\mathrm{ln}\:{x}+\mathrm{1}\right)={x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right)={x}^{{x}} +{x}^{{x}} \mathrm{ln}\:{x} \\ $$
Commented by Saham last updated on 23/Feb/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
Answered by mrW1 last updated on 23/Feb/17
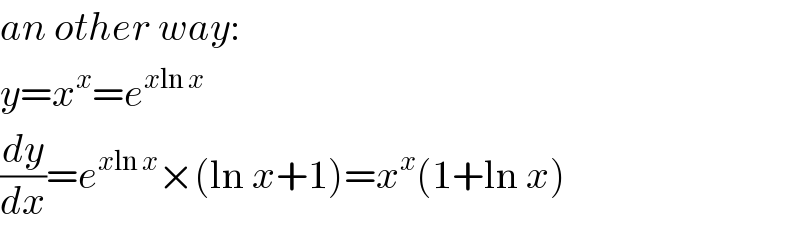
$${an}\:{other}\:{way}: \\ $$$${y}={x}^{{x}} ={e}^{{x}\mathrm{ln}\:{x}} \\ $$$$\frac{{dy}}{{dx}}={e}^{{x}\mathrm{ln}\:{x}} ×\left(\mathrm{ln}\:{x}+\mathrm{1}\right)={x}^{{x}} \left(\mathrm{1}+\mathrm{ln}\:{x}\right) \\ $$
Commented by Saham last updated on 23/Feb/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
