Question Number 5365 by sanusihammed last updated on 11/May/16

$${If}\:\:{y}\:=\:{x}^{{x}^{{x}^{{x}} } } \:\:\:.\:\:{Find}\:{dy}/{dx} \\ $$
Answered by Yozzii last updated on 11/May/16
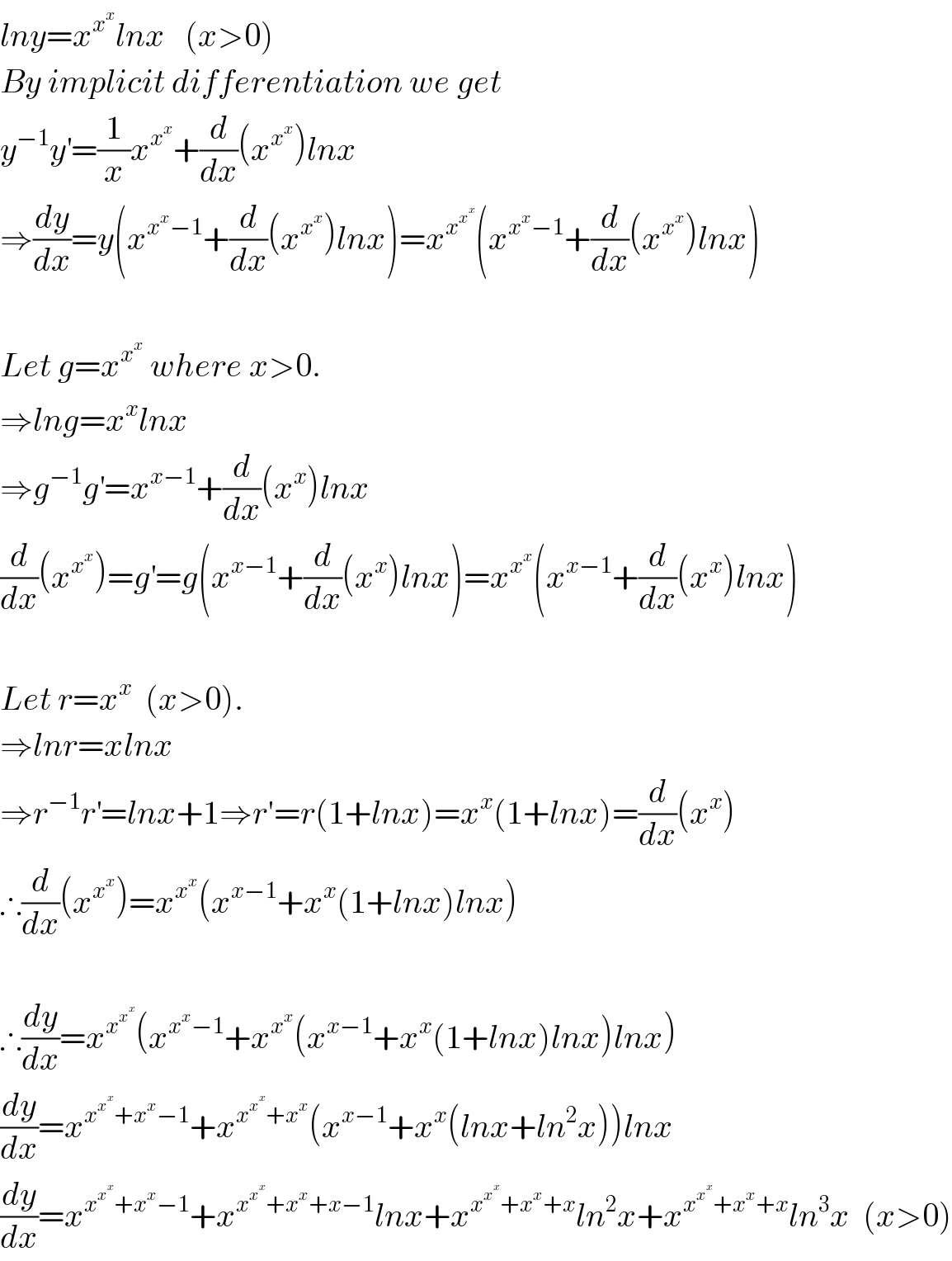
$${lny}={x}^{{x}^{{x}} } {lnx}\:\:\:\left({x}>\mathrm{0}\right) \\ $$$${By}\:{implicit}\:{differentiation}\:{we}\:{get} \\ $$$${y}^{−\mathrm{1}} {y}^{'} =\frac{\mathrm{1}}{{x}}{x}^{{x}^{{x}} } +\frac{{d}}{{dx}}\left({x}^{{x}^{{x}} } \right){lnx} \\ $$$$\Rightarrow\frac{{dy}}{{dx}}={y}\left({x}^{{x}^{{x}} −\mathrm{1}} +\frac{{d}}{{dx}}\left({x}^{{x}^{{x}} } \right){lnx}\right)={x}^{{x}^{{x}^{{x}} } } \left({x}^{{x}^{{x}} −\mathrm{1}} +\frac{{d}}{{dx}}\left({x}^{{x}^{{x}} } \right){lnx}\right) \\ $$$$ \\ $$$${Let}\:{g}={x}^{{x}^{{x}} } \:{where}\:{x}>\mathrm{0}. \\ $$$$\Rightarrow{lng}={x}^{{x}} {lnx} \\ $$$$\Rightarrow{g}^{−\mathrm{1}} {g}^{'} ={x}^{{x}−\mathrm{1}} +\frac{{d}}{{dx}}\left({x}^{{x}} \right){lnx} \\ $$$$\frac{{d}}{{dx}}\left({x}^{{x}^{{x}} } \right)={g}^{'} ={g}\left({x}^{{x}−\mathrm{1}} +\frac{{d}}{{dx}}\left({x}^{{x}} \right){lnx}\right)={x}^{{x}^{{x}} } \left({x}^{{x}−\mathrm{1}} +\frac{{d}}{{dx}}\left({x}^{{x}} \right){lnx}\right) \\ $$$$ \\ $$$${Let}\:{r}={x}^{{x}} \:\:\left({x}>\mathrm{0}\right). \\ $$$$\Rightarrow{lnr}={xlnx} \\ $$$$\Rightarrow{r}^{−\mathrm{1}} {r}^{'} ={lnx}+\mathrm{1}\Rightarrow{r}'={r}\left(\mathrm{1}+{lnx}\right)={x}^{{x}} \left(\mathrm{1}+{lnx}\right)=\frac{{d}}{{dx}}\left({x}^{{x}} \right) \\ $$$$\therefore\frac{{d}}{{dx}}\left({x}^{{x}^{{x}} } \right)={x}^{{x}^{{x}} } \left({x}^{{x}−\mathrm{1}} +{x}^{{x}} \left(\mathrm{1}+{lnx}\right){lnx}\right) \\ $$$$ \\ $$$$\therefore\frac{{dy}}{{dx}}={x}^{{x}^{{x}^{{x}} } } \left({x}^{{x}^{{x}} −\mathrm{1}} +{x}^{{x}^{{x}} } \left({x}^{{x}−\mathrm{1}} +{x}^{{x}} \left(\mathrm{1}+{lnx}\right){lnx}\right){lnx}\right) \\ $$$$\frac{{dy}}{{dx}}={x}^{{x}^{{x}^{{x}} } +{x}^{{x}} −\mathrm{1}} +{x}^{{x}^{{x}^{{x}} } +{x}^{{x}} } \left({x}^{{x}−\mathrm{1}} +{x}^{{x}} \left({lnx}+{ln}^{\mathrm{2}} {x}\right)\right){lnx} \\ $$$$\frac{{dy}}{{dx}}={x}^{{x}^{{x}^{{x}} } +{x}^{{x}} −\mathrm{1}} +{x}^{{x}^{{x}^{{x}} } +{x}^{{x}} +{x}−\mathrm{1}} {lnx}+{x}^{{x}^{{x}^{{x}} } +{x}^{{x}} +{x}} {ln}^{\mathrm{2}} {x}+{x}^{{x}^{{x}^{{x}} } +{x}^{{x}} +{x}} {ln}^{\mathrm{3}} {x}\:\:\left({x}>\mathrm{0}\right) \\ $$
Commented by sanusihammed last updated on 12/May/16

$${Thanks}\:{so}\:{much} \\ $$
Commented by sanusihammed last updated on 12/May/16

$${Thanks}\:{so}\:{much} \\ $$
