Question Number 449 by 123456 last updated on 25/Jan/15
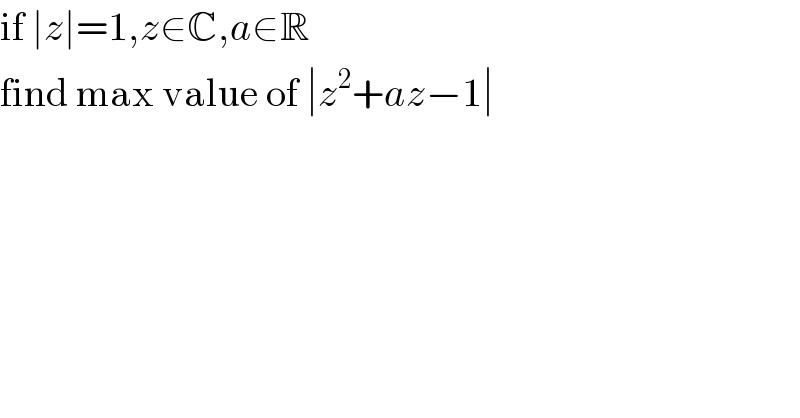
$$\mathrm{if}\:\mid{z}\mid=\mathrm{1},{z}\in\mathbb{C},{a}\in\mathbb{R} \\ $$$$\mathrm{find}\:\mathrm{max}\:\mathrm{value}\:\mathrm{of}\:\mid{z}^{\mathrm{2}} +{az}−\mathrm{1}\mid \\ $$
Answered by prakash jain last updated on 09/Jan/15

$${z}={i} \\ $$$${z}^{\mathrm{2}} =−\mathrm{1} \\ $$$${z}^{\mathrm{2}} +{az}−\mathrm{1}=−\mathrm{2}+{ai} \\ $$$$\mid−\mathrm{2}+{ai}\mid=\sqrt{\mathrm{4}+{a}^{\mathrm{2}} } \\ $$
Commented by prakash jain last updated on 09/Jan/15

$${z}={x}+{iy} \\ $$$${z}^{\mathrm{2}} ={x}^{\mathrm{2}} −{y}^{\mathrm{2}} +{i}\mathrm{2}{xy} \\ $$$${y}=\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${z}^{\mathrm{2}} =\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}{ix}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${az}={ax}+{ia}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$${z}^{\mathrm{2}} +{az}−\mathrm{1}=\mathrm{2}{x}^{\mathrm{2}} −\mathrm{1}+\mathrm{2}{ix}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }+{ax}+{ia}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1} \\ $$$$=\left(\mathrm{2}{x}^{\mathrm{2}} +{ax}−\mathrm{2}\right)+{i}\left(\mathrm{2}{x}+{a}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mid{z}^{\mathrm{2}} +{az}−\mathrm{1}\mid^{\mathrm{2}} =\left(\mathrm{2}{x}^{\mathrm{2}} +{ax}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{2}{x}+{a}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{x}^{\mathrm{4}} +{a}^{\mathrm{2}} {x}^{\mathrm{2}} +\mathrm{4}+\mathrm{4}{ax}^{\mathrm{3}} −\mathrm{8}{x}^{\mathrm{2}} −\mathrm{4}{ax}+\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{ax}+{a}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right) \\ $$$$=\mathrm{4}−\mathrm{8}{x}^{\mathrm{2}} +\mathrm{4}{x}^{\mathrm{2}} +{a}^{\mathrm{2}} \\ $$$$={a}^{\mathrm{2}} +\mathrm{4}−\mathrm{4}{x}^{\mathrm{2}} \\ $$$$\mathrm{Maximum}\:\mathrm{value}\:\mathrm{when}\:{x}=\mathrm{0} \\ $$$$\mathrm{and}\:\mathrm{is}\:\mathrm{given}\:\mathrm{by}\: \\ $$$$\mid{z}^{\mathrm{2}} +{az}−\mathrm{1}\mid=\sqrt{{a}^{\mathrm{2}} +\mathrm{4}} \\ $$
