Menu Close

If-z-C-satisfies-z-3-z-3-2-then-maximum-possible-value-of-z-z-1-is-

Tinku Tara 0 Comments
Pin




Question Number 8721 by swapnil last updated on 24/Oct/16
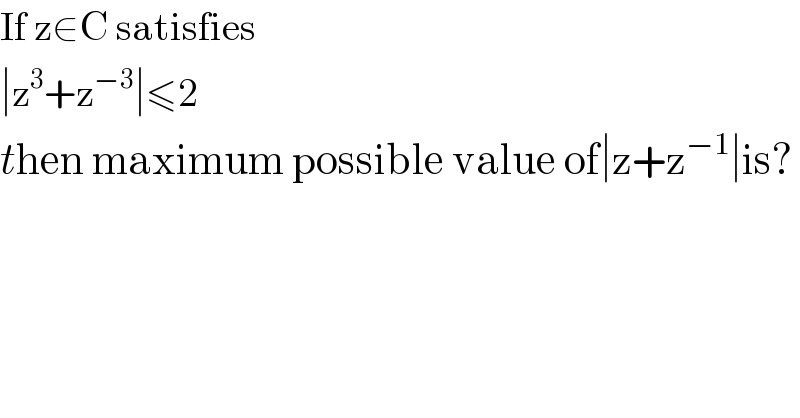
If z∈C satisfies ∣z^3 +z^(−3) ∣≤2 then maximum possible value of∣z+z^(−1) ∣is?
$$\mathrm{If}\:\mathrm{z}\in\mathrm{C}\:\mathrm{satisfies} \\ $$$$\mid\mathrm{z}^{\mathrm{3}} +\mathrm{z}^{−\mathrm{3}} \mid\leqslant\mathrm{2} \\ $$$${t}\mathrm{hen}\:\mathrm{maximum}\:\mathrm{possible}\:\mathrm{value}\:\mathrm{of}\mid\mathrm{z}+\mathrm{z}^{−\mathrm{1}} \mid\mathrm{is}? \\ $$
Commented by 123456 last updated on 24/Oct/16
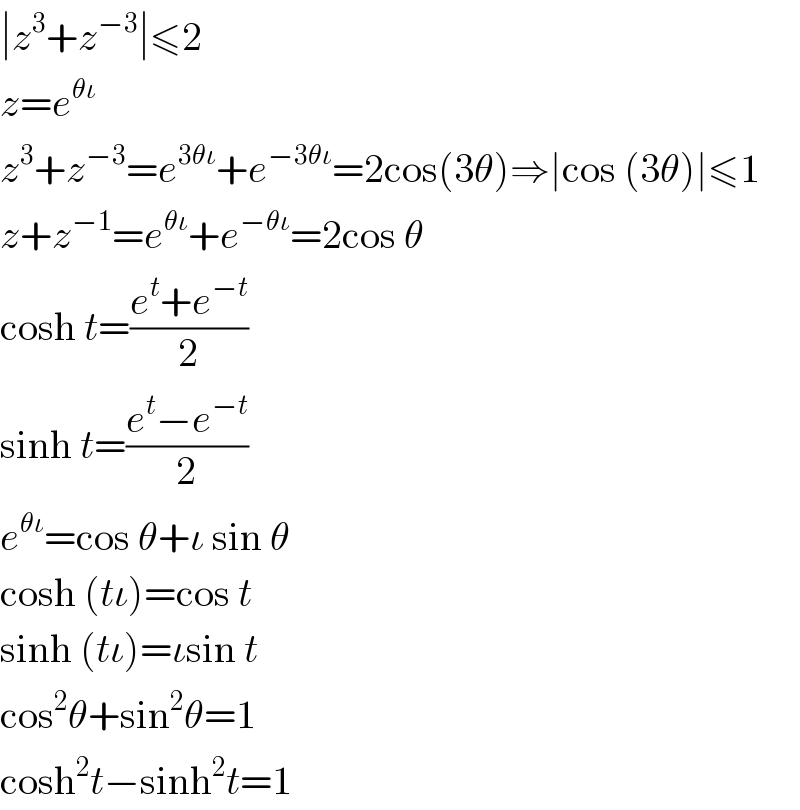
∣z^3 +z^(−3) ∣≤2 z=e^(θι) z^3 +z^(−3) =e^(3θι) +e^(−3θι) =2cos(3θ)⇒∣cos (3θ)∣≤1 z+z^(−1) =e^(θι) +e^(−θι) =2cos θ cosh t=((e^t +e^(−t) )/2) sinh t=((e^t −e^(−t) )/2) e^(θι) =cos θ+ι sin θ cosh (tι)=cos t sinh (tι)=ιsin t cos^2 θ+sin^2 θ=1 cosh^2 t−sinh^2 t=1
$$\mid{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} \mid\leqslant\mathrm{2} \\ $$$${z}={e}^{\theta\iota} \\ $$$${z}^{\mathrm{3}} +{z}^{−\mathrm{3}} ={e}^{\mathrm{3}\theta\iota} +{e}^{−\mathrm{3}\theta\iota} =\mathrm{2cos}\left(\mathrm{3}\theta\right)\Rightarrow\mid\mathrm{cos}\:\left(\mathrm{3}\theta\right)\mid\leqslant\mathrm{1} \\ $$$${z}+{z}^{−\mathrm{1}} ={e}^{\theta\iota} +{e}^{−\theta\iota} =\mathrm{2cos}\:\theta \\ $$$$\mathrm{cosh}\:{t}=\frac{{e}^{{t}} +{e}^{−{t}} }{\mathrm{2}} \\ $$$$\mathrm{sinh}\:{t}=\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}} \\ $$$${e}^{\theta\iota} =\mathrm{cos}\:\theta+\iota\:\mathrm{sin}\:\theta\: \\ $$$$\mathrm{cosh}\:\left({t}\iota\right)=\mathrm{cos}\:{t} \\ $$$$\mathrm{sinh}\:\left({t}\iota\right)=\iota\mathrm{sin}\:{t} \\ $$$$\mathrm{cos}^{\mathrm{2}} \theta+\mathrm{sin}^{\mathrm{2}} \theta=\mathrm{1} \\ $$$$\mathrm{cosh}^{\mathrm{2}} {t}−\mathrm{sinh}^{\mathrm{2}} {t}=\mathrm{1} \\ $$
Commented by prakash jain last updated on 24/Oct/16
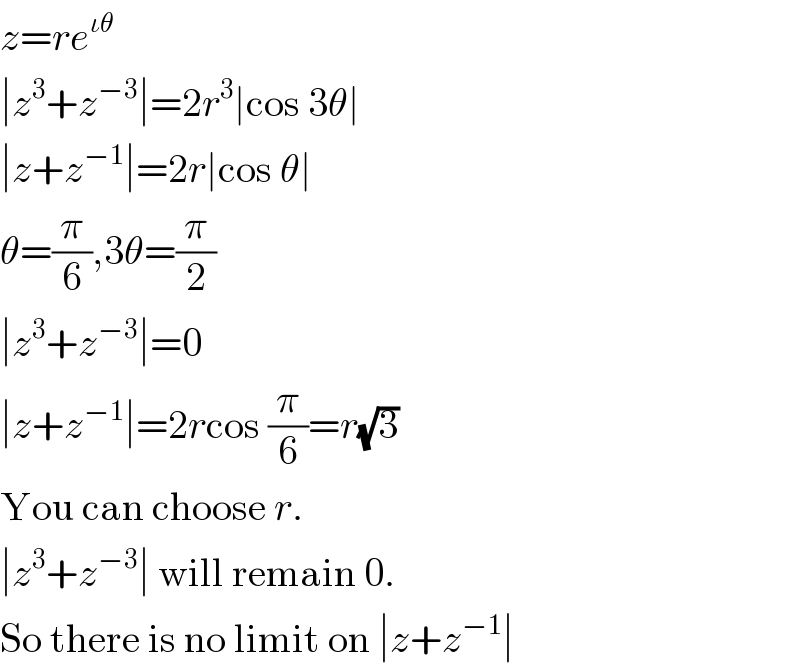
z=re^(ιθ) ∣z^3 +z^(−3) ∣=2r^3 ∣cos 3θ∣ ∣z+z^(−1) ∣=2r∣cos θ∣ θ=(π/6),3θ=(π/2) ∣z^3 +z^(−3) ∣=0 ∣z+z^(−1) ∣=2rcos (π/6)=r(√3) You can choose r. ∣z^3 +z^(−3) ∣ will remain 0. So there is no limit on ∣z+z^(−1) ∣
$${z}={re}^{\iota\theta} \\ $$$$\mid{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} \mid=\mathrm{2}{r}^{\mathrm{3}} \mid\mathrm{cos}\:\mathrm{3}\theta\mid \\ $$$$\mid{z}+{z}^{−\mathrm{1}} \mid=\mathrm{2}{r}\mid\mathrm{cos}\:\theta\mid \\ $$$$\theta=\frac{\pi}{\mathrm{6}},\mathrm{3}\theta=\frac{\pi}{\mathrm{2}} \\ $$$$\mid{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} \mid=\mathrm{0} \\ $$$$\mid{z}+{z}^{−\mathrm{1}} \mid=\mathrm{2}{r}\mathrm{cos}\:\frac{\pi}{\mathrm{6}}={r}\sqrt{\mathrm{3}} \\ $$$$\mathrm{You}\:\mathrm{can}\:\mathrm{choose}\:{r}. \\ $$$$\mid{z}^{\mathrm{3}} +{z}^{−\mathrm{3}} \mid\:\mathrm{will}\:\mathrm{remain}\:\mathrm{0}. \\ $$$$\mathrm{So}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{limit}\:\mathrm{on}\:\mid{z}+{z}^{−\mathrm{1}} \mid \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *