Question Number 7739 by upendrakishor99@gmail.com last updated on 13/Sep/16
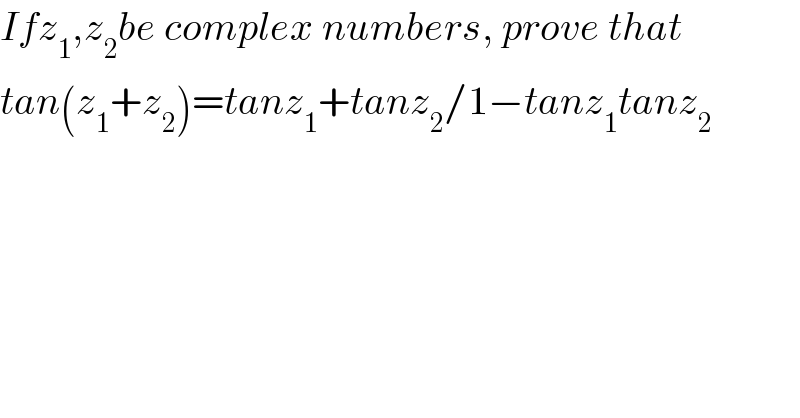
$${Ifz}_{\mathrm{1}} ,{z}_{\mathrm{2}} {be}\:{complex}\:{numbers},\:{prove}\:{that} \\ $$$${tan}\left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right)={tanz}_{\mathrm{1}} +{tanz}_{\mathrm{2}} /\mathrm{1}−{tanz}_{\mathrm{1}} {tanz}_{\mathrm{2}} \\ $$$$ \\ $$$$ \\ $$
Commented by prakash jain last updated on 14/Sep/16
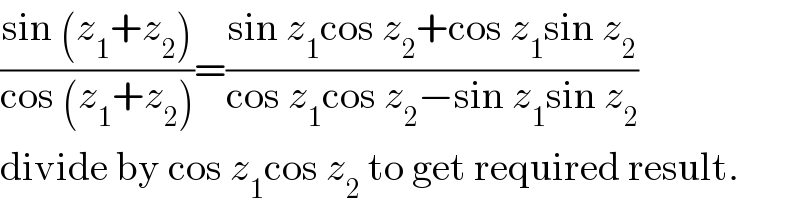
$$\frac{\mathrm{sin}\:\left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right)}{\mathrm{cos}\:\left({z}_{\mathrm{1}} +{z}_{\mathrm{2}} \right)}=\frac{\mathrm{sin}\:{z}_{\mathrm{1}} \mathrm{cos}\:{z}_{\mathrm{2}} +\mathrm{cos}\:{z}_{\mathrm{1}} \mathrm{sin}\:{z}_{\mathrm{2}} }{\mathrm{cos}\:{z}_{\mathrm{1}} \mathrm{cos}\:{z}_{\mathrm{2}} −\mathrm{sin}\:{z}_{\mathrm{1}} \mathrm{sin}\:{z}_{\mathrm{2}} } \\ $$$$\mathrm{divide}\:\mathrm{by}\:\mathrm{cos}\:{z}_{\mathrm{1}} \mathrm{cos}\:{z}_{\mathrm{2}} \:\mathrm{to}\:\mathrm{get}\:\mathrm{required}\:\mathrm{result}. \\ $$
