Menu Close

In-a-equilateral-triangle-ABC-whose-side-is-a-the-points-M-and-N-are-taken-on-the-side-BC-such-that-the-triangles-ABM-AMN-and-ANC-have-the-same-perimeter-Calculate-the-distances-from-vertex-A-to-

Tinku Tara 0 Comments
Pin




Question Number 68664 by Maclaurin Stickker last updated on 14/Sep/19
In a equilateral triangle ABC whose side is a, the points M and N are taken on the side BC, such that the triangles ABM, AMN and ANC have the same perimeter. Calculate the distances from vertex A to points M and N. (solve in detail.)
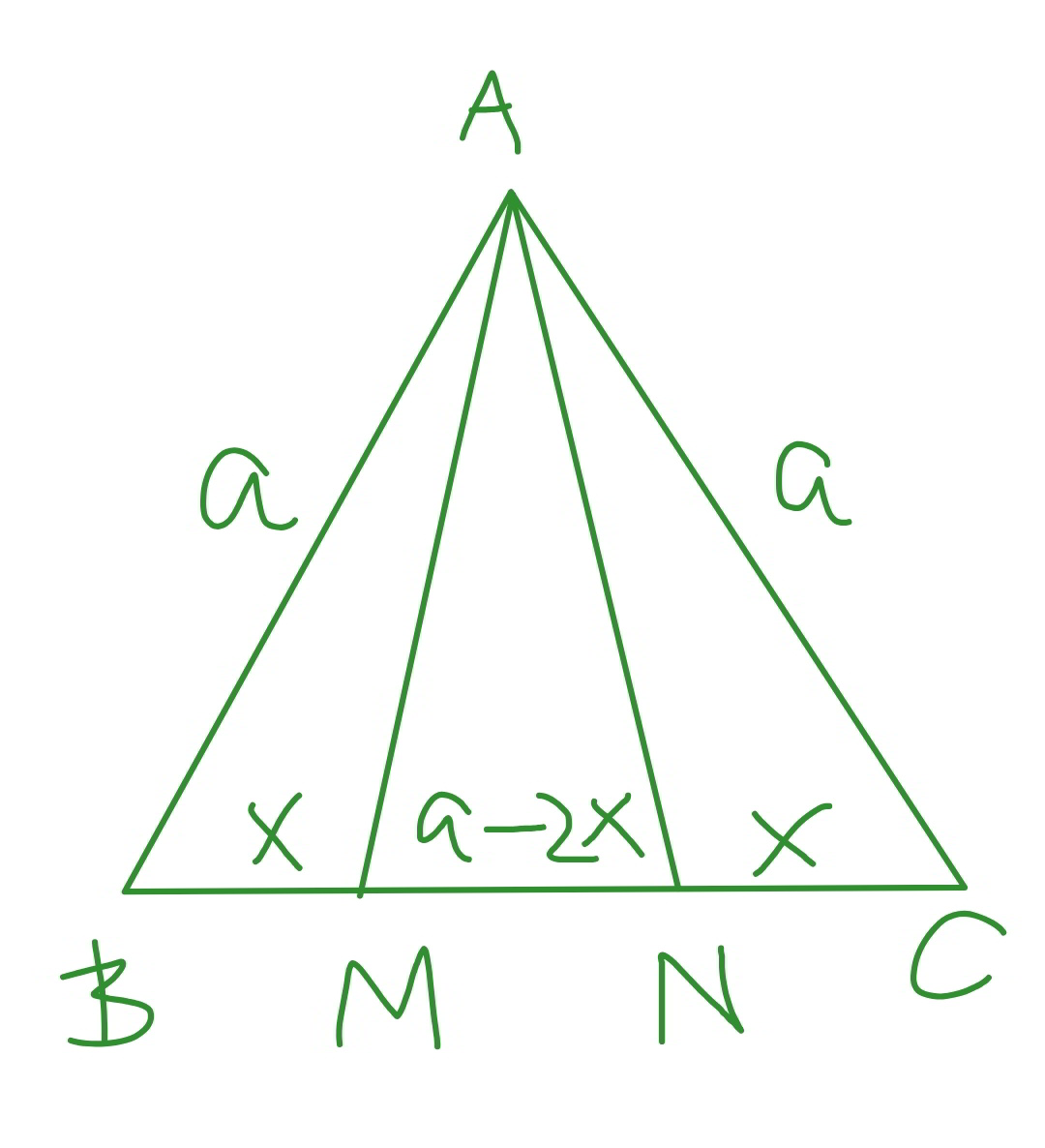
$$\mathrm{In}\:\mathrm{a}\:\mathrm{equilateral}\:\mathrm{triangle}\:{ABC}\:\mathrm{whose} \\ $$$$\mathrm{side}\:\mathrm{is}\:\boldsymbol{{a}},\:\mathrm{the}\:\mathrm{points}\:{M}\:\mathrm{and}\:{N}\:\mathrm{are}\:\mathrm{taken} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{side}\:{BC},\:\mathrm{such}\:\mathrm{that}\:\mathrm{the}\:\mathrm{triangles} \\ $$$${ABM},\:{AMN}\:\mathrm{and}\:{ANC}\:\mathrm{have}\:\mathrm{the}\:\mathrm{same}\: \\ $$$$\mathrm{perimeter}.\:\mathrm{Calculate}\:\mathrm{the}\:\mathrm{distances}\:\mathrm{from} \\ $$$$\mathrm{vertex}\:{A}\:\mathrm{to}\:\mathrm{points}\:{M}\:\mathrm{and}\:{N}. \\ $$$$\left(\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{detail}}.\right) \\ $$
Answered by mr W last updated on 14/Sep/19
Commented by mr W last updated on 14/Sep/19
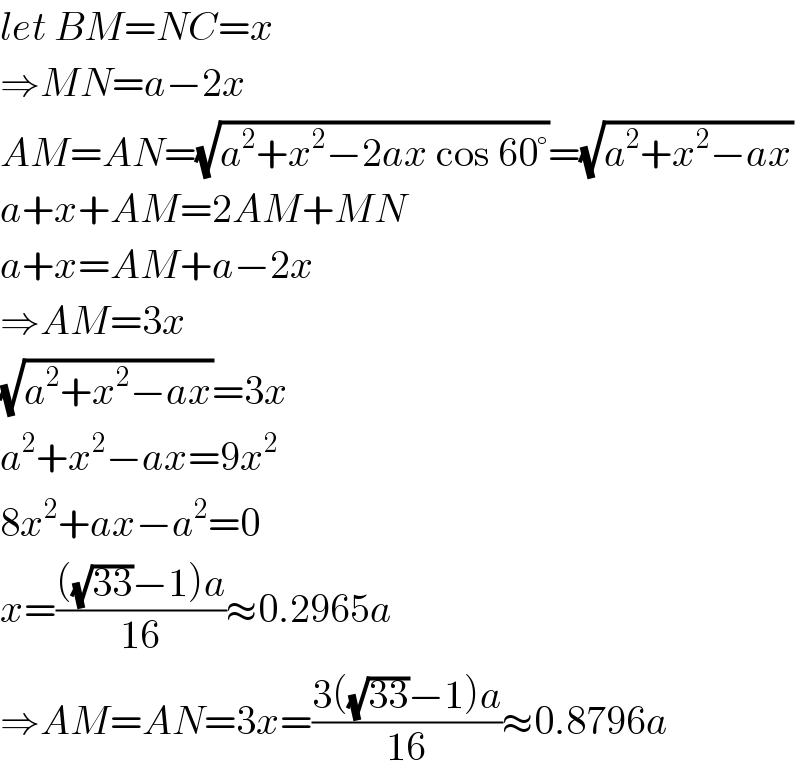
let BM=NC=x ⇒MN=a−2x AM=AN=(√(a^2 +x^2 −2ax cos 60°))=(√(a^2 +x^2 −ax)) a+x+AM=2AM+MN a+x=AM+a−2x ⇒AM=3x (√(a^2 +x^2 −ax))=3x a^2 +x^2 −ax=9x^2 8x^2 +ax−a^2 =0 x=((((√(33))−1)a)/(16))≈0.2965a ⇒AM=AN=3x=((3((√(33))−1)a)/(16))≈0.8796a
$${let}\:{BM}={NC}={x} \\ $$$$\Rightarrow{MN}={a}−\mathrm{2}{x} \\ $$$${AM}={AN}=\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{ax}\:\mathrm{cos}\:\mathrm{60}°}=\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} −{ax}} \\ $$$${a}+{x}+{AM}=\mathrm{2}{AM}+{MN} \\ $$$${a}+{x}={AM}+{a}−\mathrm{2}{x} \\ $$$$\Rightarrow{AM}=\mathrm{3}{x} \\ $$$$\sqrt{{a}^{\mathrm{2}} +{x}^{\mathrm{2}} −{ax}}=\mathrm{3}{x} \\ $$$${a}^{\mathrm{2}} +{x}^{\mathrm{2}} −{ax}=\mathrm{9}{x}^{\mathrm{2}} \\ $$$$\mathrm{8}{x}^{\mathrm{2}} +{ax}−{a}^{\mathrm{2}} =\mathrm{0} \\ $$$${x}=\frac{\left(\sqrt{\mathrm{33}}−\mathrm{1}\right){a}}{\mathrm{16}}\approx\mathrm{0}.\mathrm{2965}{a} \\ $$$$\Rightarrow{AM}={AN}=\mathrm{3}{x}=\frac{\mathrm{3}\left(\sqrt{\mathrm{33}}−\mathrm{1}\right){a}}{\mathrm{16}}\approx\mathrm{0}.\mathrm{8796}{a} \\ $$
Commented by Rasheed.Sindhi last updated on 15/Sep/19
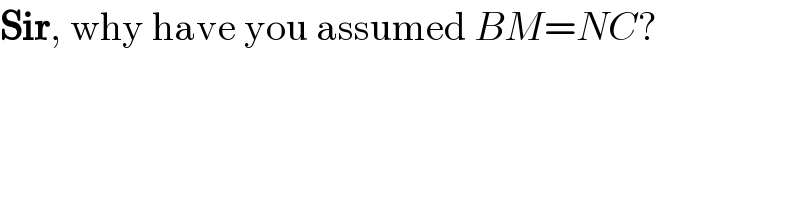
Sir, why have you assumed BM=NC?
$$\boldsymbol{\mathrm{Sir}},\:\mathrm{why}\:\mathrm{have}\:\mathrm{you}\:\mathrm{assumed}\:{BM}={NC}? \\ $$
Commented by mr W last updated on 15/Sep/19
the assumption is based on symmetry. certainly it can also be proved that BM must be equal to NC.
$${the}\:{assumption}\:{is}\:{based}\:{on}\:{symmetry}. \\ $$$${certainly}\:{it}\:{can}\:{also}\:\:{be}\:{proved}\:{that} \\ $$$${BM}\:{must}\:{be}\:{equal}\:{to}\:{NC}. \\ $$
Commented by mr W last updated on 15/Sep/19
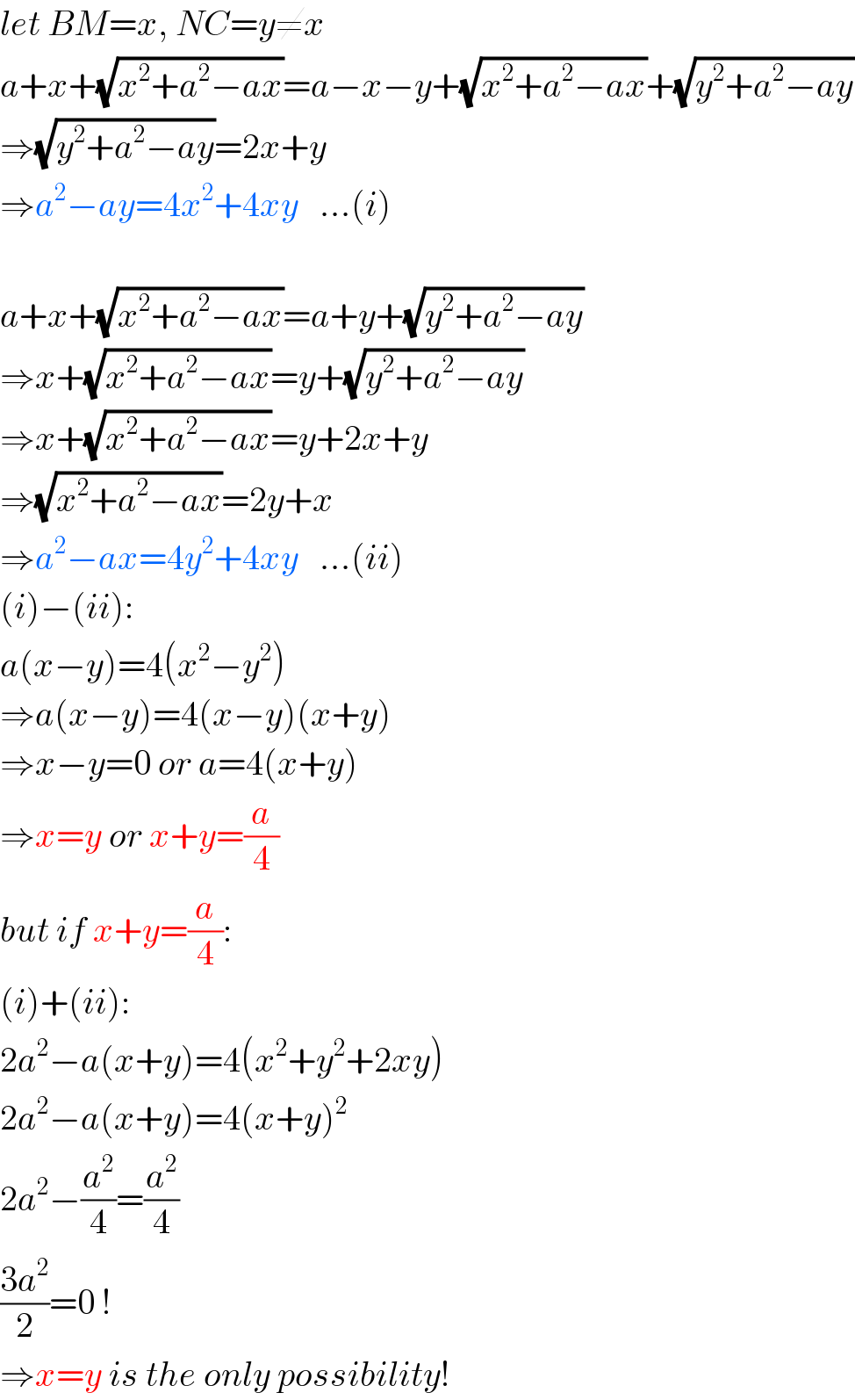
let BM=x, NC=y≠x a+x+(√(x^2 +a^2 −ax))=a−x−y+(√(x^2 +a^2 −ax))+(√(y^2 +a^2 −ay)) ⇒(√(y^2 +a^2 −ay))=2x+y ⇒a^2 −ay=4x^2 +4xy ...(i) a+x+(√(x^2 +a^2 −ax))=a+y+(√(y^2 +a^2 −ay)) ⇒x+(√(x^2 +a^2 −ax))=y+(√(y^2 +a^2 −ay)) ⇒x+(√(x^2 +a^2 −ax))=y+2x+y ⇒(√(x^2 +a^2 −ax))=2y+x ⇒a^2 −ax=4y^2 +4xy ...(ii) (i)−(ii): a(x−y)=4(x^2 −y^2 ) ⇒a(x−y)=4(x−y)(x+y) ⇒x−y=0 or a=4(x+y) ⇒x=y or x+y=(a/4) but if x+y=(a/4): (i)+(ii): 2a^2 −a(x+y)=4(x^2 +y^2 +2xy) 2a^2 −a(x+y)=4(x+y)^2 2a^2 −(a^2 /4)=(a^2 /4) ((3a^2 )/2)=0 ! ⇒x=y is the only possibility!
$${let}\:{BM}={x},\:{NC}={y}\neq{x} \\ $$$${a}+{x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ax}}={a}−{x}−{y}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ax}}+\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ay}} \\ $$$$\Rightarrow\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ay}}=\mathrm{2}{x}+{y} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{ay}=\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{xy}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${a}+{x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ax}}={a}+{y}+\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ay}} \\ $$$$\Rightarrow{x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ax}}={y}+\sqrt{{y}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ay}} \\ $$$$\Rightarrow{x}+\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ax}}={y}+\mathrm{2}{x}+{y} \\ $$$$\Rightarrow\sqrt{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} −{ax}}=\mathrm{2}{y}+{x} \\ $$$$\Rightarrow{a}^{\mathrm{2}} −{ax}=\mathrm{4}{y}^{\mathrm{2}} +\mathrm{4}{xy}\:\:\:…\left({ii}\right) \\ $$$$\left({i}\right)−\left({ii}\right): \\ $$$${a}\left({x}−{y}\right)=\mathrm{4}\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right) \\ $$$$\Rightarrow{a}\left({x}−{y}\right)=\mathrm{4}\left({x}−{y}\right)\left({x}+{y}\right) \\ $$$$\Rightarrow{x}−{y}=\mathrm{0}\:{or}\:{a}=\mathrm{4}\left({x}+{y}\right) \\ $$$$\Rightarrow{x}={y}\:{or}\:{x}+{y}=\frac{{a}}{\mathrm{4}} \\ $$$${but}\:{if}\:{x}+{y}=\frac{{a}}{\mathrm{4}}: \\ $$$$\left({i}\right)+\left({ii}\right): \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −{a}\left({x}+{y}\right)=\mathrm{4}\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{2}{xy}\right) \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −{a}\left({x}+{y}\right)=\mathrm{4}\left({x}+{y}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} −\frac{{a}^{\mathrm{2}} }{\mathrm{4}}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{0}\:! \\ $$$$\Rightarrow{x}={y}\:{is}\:{the}\:{only}\:{possibility}! \\ $$
Commented by Rasheed.Sindhi last updated on 15/Sep/19
ThαnX a lot sir. You′re very deep in geometry also!
$$\mathcal{T}{h}\alpha{n}\mathcal{X}\:{a}\:{lot}\:{sir}.\:{You}'\mathrm{re}\:{very}\:{deep} \\ $$$${in}\:{geometry}\:{also}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *