Question Number 76455 by Maclaurin Stickker last updated on 27/Dec/19

$${In}\:{a}\:{triangle}\:{whose}\:{sides}\:{measure} \\ $$$$\mathrm{5}\:{cm},\:\mathrm{6}\:{cm},\:{and}\:\:\mathrm{7}\:{cm}\:{a}\:{point}\:{P},\:{inside} \\ $$$${the}\:{triangle}\:{is}\:\mathrm{2}\:{cm}\:{from}\:{de}\:{long}\:{side} \\ $$$$\mathrm{5}\:{cm}\:{and}\:\mathrm{3}\:{cm}\:{from}\:{the}\:{long}\:{side} \\ $$$$\mathrm{6}\:{cm}.\:{What}\:{is}\:{the}\:{distance}\:{from}\:{P} \\ $$$${beside}\:\mathrm{7}\:{cm}\:{side}? \\ $$
Commented by MJS last updated on 27/Dec/19

$$\mathrm{we}\:\mathrm{can}\:\mathrm{construct}\:\mathrm{it}\:\Rightarrow\:\mathrm{we}\:\mathrm{can}\:\mathrm{calculate}\:\mathrm{it} \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:\mathrm{draw}\:\mathrm{the}\:\mathrm{triangle} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{draw}\:\mathrm{parallels}\:\mathrm{to}\:\mathrm{the}\:\mathrm{sides}\:\Rightarrow\:{P} \\ $$$$\left(\mathrm{3}\right)\:\mathrm{measure}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{between}\:{P}\:\mathrm{and} \\ $$$$\:\:\:\:\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{side} \\ $$
Commented by Maclaurin Stickker last updated on 27/Dec/19

$${thanks} \\ $$
Answered by mr W last updated on 27/Dec/19
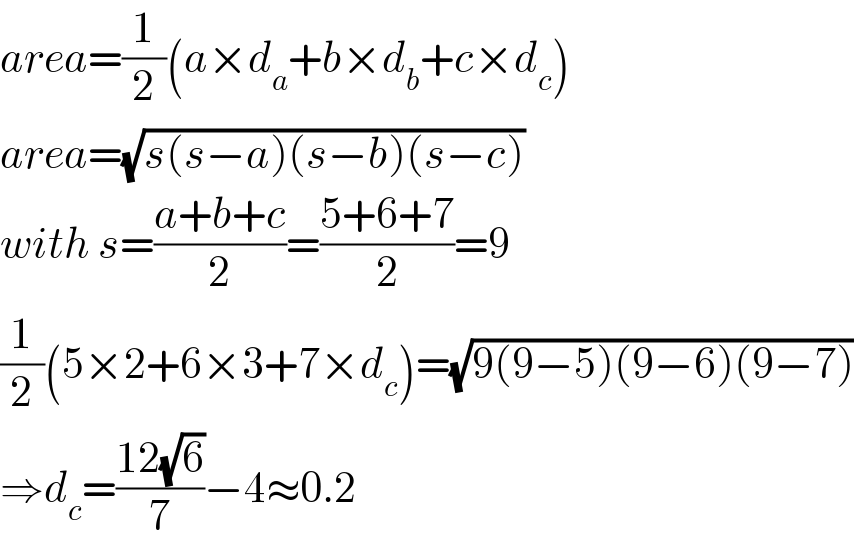
$${area}=\frac{\mathrm{1}}{\mathrm{2}}\left({a}×{d}_{{a}} +{b}×{d}_{{b}} +{c}×{d}_{{c}} \right) \\ $$$${area}=\sqrt{{s}\left({s}−{a}\right)\left({s}−{b}\right)\left({s}−{c}\right)} \\ $$$${with}\:{s}=\frac{{a}+{b}+{c}}{\mathrm{2}}=\frac{\mathrm{5}+\mathrm{6}+\mathrm{7}}{\mathrm{2}}=\mathrm{9} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{5}×\mathrm{2}+\mathrm{6}×\mathrm{3}+\mathrm{7}×{d}_{{c}} \right)=\sqrt{\mathrm{9}\left(\mathrm{9}−\mathrm{5}\right)\left(\mathrm{9}−\mathrm{6}\right)\left(\mathrm{9}−\mathrm{7}\right)} \\ $$$$\Rightarrow{d}_{{c}} =\frac{\mathrm{12}\sqrt{\mathrm{6}}}{\mathrm{7}}−\mathrm{4}\approx\mathrm{0}.\mathrm{2} \\ $$
Commented by mr W last updated on 27/Dec/19
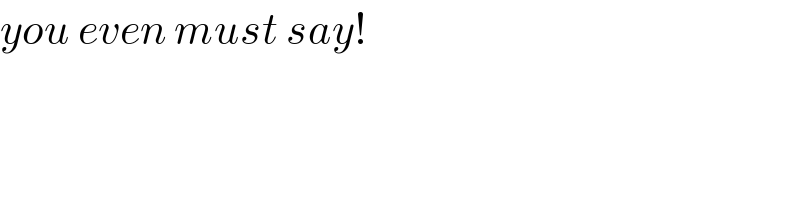
$${you}\:{even}\:{must}\:{say}! \\ $$
Commented by Maclaurin Stickker last updated on 27/Dec/19
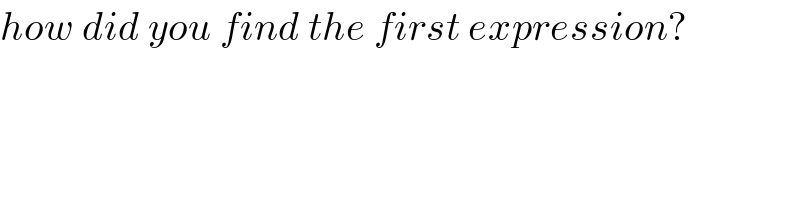
$${how}\:{did}\:{you}\:{find}\:{the}\:{first}\:{expression}? \\ $$
Commented by mr W last updated on 27/Dec/19

Commented by mr W last updated on 27/Dec/19
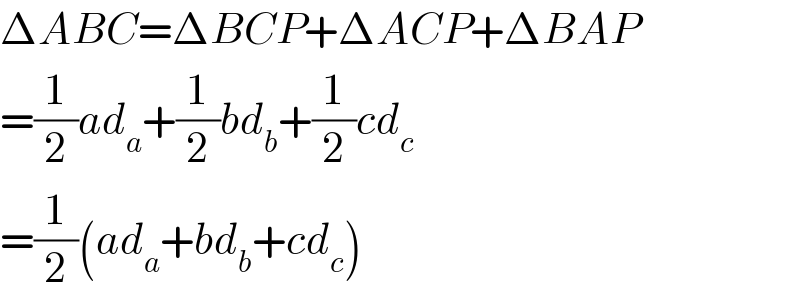
$$\Delta{ABC}=\Delta{BCP}+\Delta{ACP}+\Delta{BAP} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ad}_{{a}} +\frac{\mathrm{1}}{\mathrm{2}}{bd}_{{b}} +\frac{\mathrm{1}}{\mathrm{2}}{cd}_{{c}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({ad}_{{a}} +{bd}_{{b}} +{cd}_{{c}} \right) \\ $$
Commented by Maclaurin Stickker last updated on 27/Dec/19
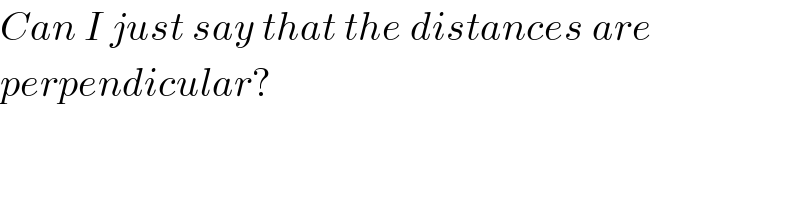
$${Can}\:{I}\:{just}\:{say}\:{that}\:{the}\:{distances}\:{are} \\ $$$${perpendicular}? \\ $$
