Question Number 9986 by lepan last updated on 20/Jan/17
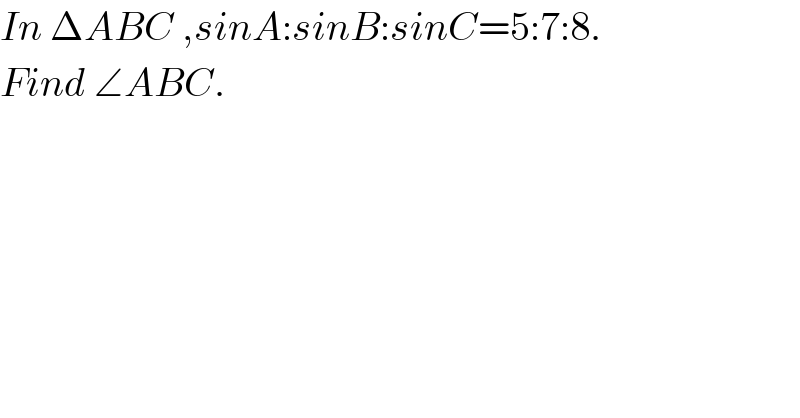
$${In}\:\Delta{ABC}\:,{sinA}:{sinB}:{sinC}=\mathrm{5}:\mathrm{7}:\mathrm{8}. \\ $$$${Find}\:\angle{ABC}. \\ $$
Answered by mrW1 last updated on 20/Jan/17
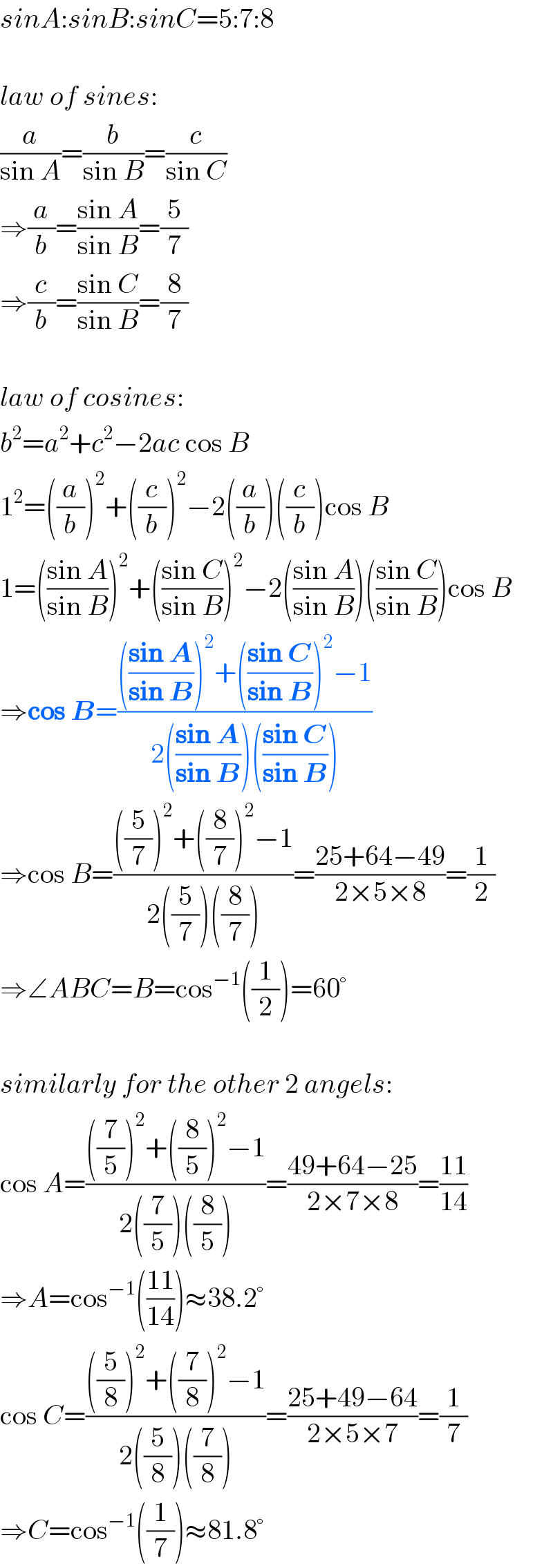
$${sinA}:{sinB}:{sinC}=\mathrm{5}:\mathrm{7}:\mathrm{8} \\ $$$$ \\ $$$${law}\:{of}\:{sines}: \\ $$$$\frac{{a}}{\mathrm{sin}\:{A}}=\frac{{b}}{\mathrm{sin}\:{B}}=\frac{{c}}{\mathrm{sin}\:{C}} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{B}}=\frac{\mathrm{5}}{\mathrm{7}} \\ $$$$\Rightarrow\frac{{c}}{{b}}=\frac{\mathrm{sin}\:{C}}{\mathrm{sin}\:{B}}=\frac{\mathrm{8}}{\mathrm{7}} \\ $$$$ \\ $$$${law}\:{of}\:{cosines}: \\ $$$${b}^{\mathrm{2}} ={a}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}{ac}\:\mathrm{cos}\:{B} \\ $$$$\mathrm{1}^{\mathrm{2}} =\left(\frac{{a}}{{b}}\right)^{\mathrm{2}} +\left(\frac{{c}}{{b}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{{a}}{{b}}\right)\left(\frac{{c}}{{b}}\right)\mathrm{cos}\:{B} \\ $$$$\mathrm{1}=\left(\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{B}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{sin}\:{C}}{\mathrm{sin}\:{B}}\right)^{\mathrm{2}} −\mathrm{2}\left(\frac{\mathrm{sin}\:{A}}{\mathrm{sin}\:{B}}\right)\left(\frac{\mathrm{sin}\:{C}}{\mathrm{sin}\:{B}}\right)\mathrm{cos}\:{B} \\ $$$$\Rightarrow\boldsymbol{\mathrm{cos}}\:\boldsymbol{{B}}=\frac{\left(\frac{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{A}}}{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{B}}}\right)^{\mathrm{2}} +\left(\frac{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{C}}}{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{B}}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\left(\frac{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{A}}}{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{B}}}\right)\left(\frac{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{C}}}{\boldsymbol{\mathrm{sin}}\:\boldsymbol{{B}}}\right)} \\ $$$$\Rightarrow\mathrm{cos}\:{B}=\frac{\left(\frac{\mathrm{5}}{\mathrm{7}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{8}}{\mathrm{7}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{5}}{\mathrm{7}}\right)\left(\frac{\mathrm{8}}{\mathrm{7}}\right)}=\frac{\mathrm{25}+\mathrm{64}−\mathrm{49}}{\mathrm{2}×\mathrm{5}×\mathrm{8}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\angle{ABC}={B}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\mathrm{60}° \\ $$$$ \\ $$$${similarly}\:{for}\:{the}\:{other}\:\mathrm{2}\:{angels}: \\ $$$$\mathrm{cos}\:{A}=\frac{\left(\frac{\mathrm{7}}{\mathrm{5}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{8}}{\mathrm{5}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{7}}{\mathrm{5}}\right)\left(\frac{\mathrm{8}}{\mathrm{5}}\right)}=\frac{\mathrm{49}+\mathrm{64}−\mathrm{25}}{\mathrm{2}×\mathrm{7}×\mathrm{8}}=\frac{\mathrm{11}}{\mathrm{14}} \\ $$$$\Rightarrow{A}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{11}}{\mathrm{14}}\right)\approx\mathrm{38}.\mathrm{2}° \\ $$$$\mathrm{cos}\:{C}=\frac{\left(\frac{\mathrm{5}}{\mathrm{8}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{7}}{\mathrm{8}}\right)^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\left(\frac{\mathrm{5}}{\mathrm{8}}\right)\left(\frac{\mathrm{7}}{\mathrm{8}}\right)}=\frac{\mathrm{25}+\mathrm{49}−\mathrm{64}}{\mathrm{2}×\mathrm{5}×\mathrm{7}}=\frac{\mathrm{1}}{\mathrm{7}} \\ $$$$\Rightarrow{C}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{7}}\right)\approx\mathrm{81}.\mathrm{8}° \\ $$
