In-mathematics-I-have-worked-with-and-e-g-k-1-x-k-1-2-x-x-1-k-1-x-k-k-I-have-never-worked-with-I-am-curious-as-to-what-it-is-Is-it-another-notation-form-Does-k-1-x-k

FacebookTweetPin

Question Number 4650 by FilupSmith last updated on 18/Feb/16

$$\mathrm{In}\mathrm{mathematics}\mathrm{I}\mathrm{have}\mathrm{worked}\mathrm{with}:$$$$\mathrm{\Sigma }\mathrm{and}\mathrm{\Pi }.$$$$e.g.$$$$\underset{k=1}{\sum ^x}k=\frac{1}{2}x(x+1)$$$$\underset{k=1}{\prod ^x}k=k!$$$$$$$$\mathrm{I}\mathrm{have}\mathrm{never}\mathrm{worked}\mathrm{with}\coprod .\mathrm{I}\mathrm{am}\mathrm{curious}$$$$\mathrm{as}\mathrm{to}\mathrm{what}\mathrm{it}\mathrm{is}.\mathrm{Is}\mathrm{it}\mathrm{another}\mathrm{notation}\mathrm{form}?$$$$\mathrm{Does}\underset{k=1}{\coprod ^x}k\mathrm{exist}?$$

Commented by Yozzii last updated on 19/Feb/16

Commented by Yozzii last updated on 19/Feb/16

$$Categorytheory;source:wikipedia$$

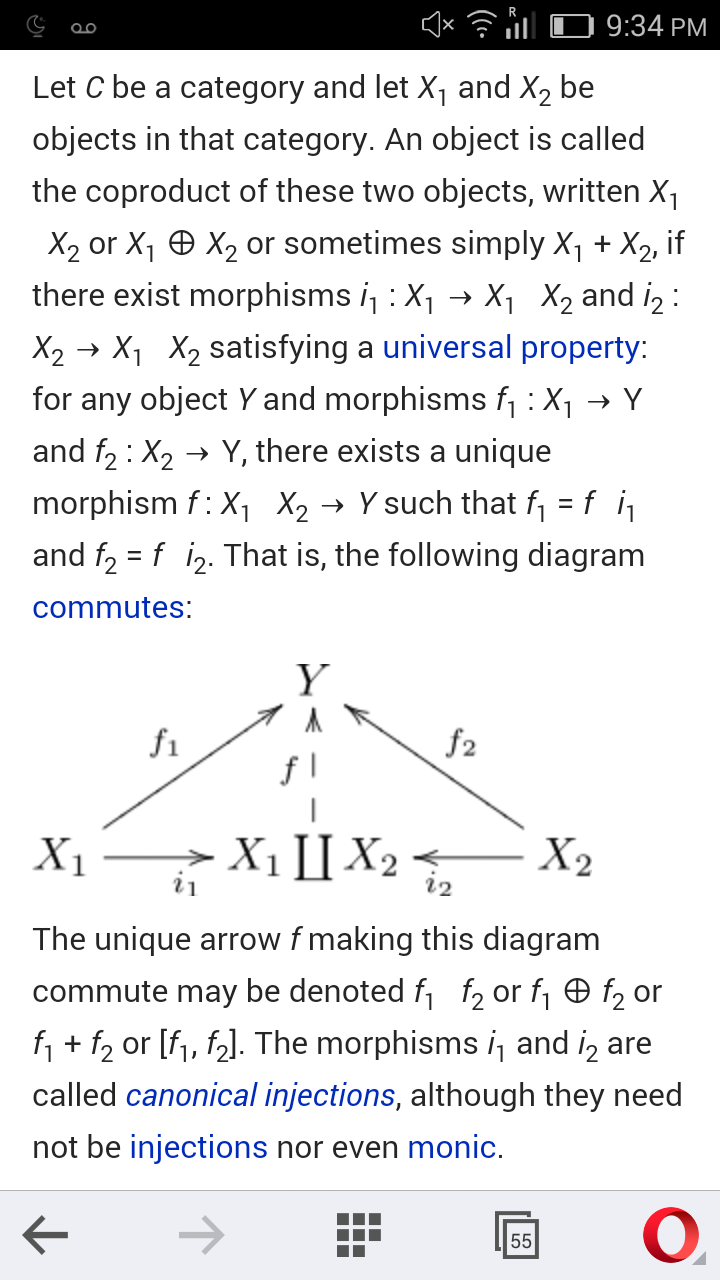
Commented by Yozzii last updated on 19/Feb/16

Commented by Yozzii last updated on 19/Feb/16

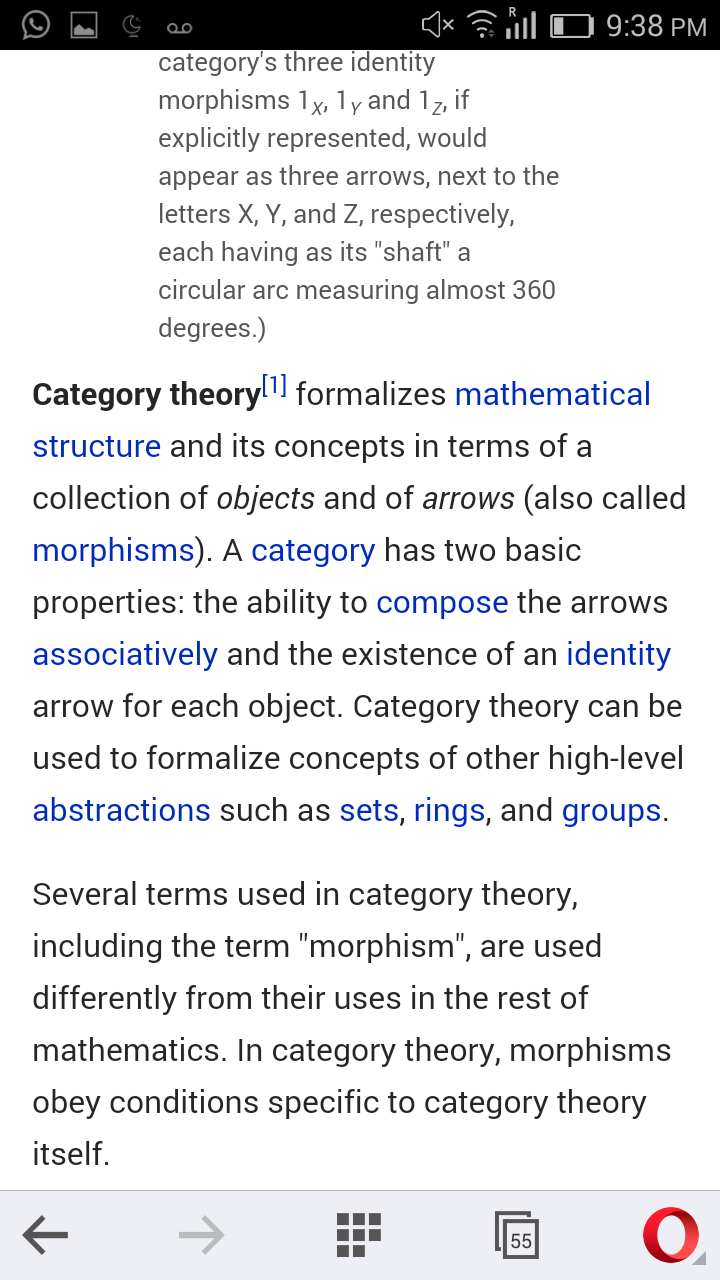
Commented by FilupSmith last updated on 19/Feb/16

$$\mathrm{Very}\mathrm{interesting}!$$

Commented by 2closedStringsMeet last updated on 19/Feb/16

$$Awesome!Indeedveryinteresting.$$

Answered by 2closedStringsMeet last updated on 19/Feb/16

$$itislikelythedisjuntivesumoperator.$$$$Logicaloperator\left[or\right]\dots$$

Commented by FilupSmith last updated on 19/Feb/16

$$\mathrm{I}\mathrm{see}.\mathrm{Thanks}!$$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com

FacebookTweetPin