In-my-textbook-its-written-In-applying-the-nth-term-test-we-can-see-that-n-1-1-n-1-diverges-because-lim-n-1-n-1-does-not-exist-But-then-why-n-1-1-n-1-1-n-2-

Question Number 68161 by Learner-123 last updated on 06/Sep/19

I n m y t e x t b o o k i t s w r i t t e n :

I n a p p l y i n g t h e n t h - t e r m t e s t w e

c a n s e e t h a t :

\underset{n = 1}{\sum^{\infty}} {(- 1)}^{n + 1} d i v e r g e s b e c a u s e

{l i m}_{n \to \infty} {(- 1)}^{n + 1} d o e s n o t e x i s t .

B u t t h e n w h y \underset{n = 1}{\sum^{\infty}} {(- 1)}^{n + 1} \frac{1}{n^{2}}, \underset{n = 1}{\sum^{\infty}} {(- 1)}^{n + 1} \frac{1}{l n (n)}

c o n v e r g e s ?

Commented by Learner-123 last updated on 06/Sep/19

I c a n s a y w i t h t h e s i m i l a r a r g u m e n t

t h a t l i m i t d o e s n o t e x i s t \Rightarrow d i v e r g e s .

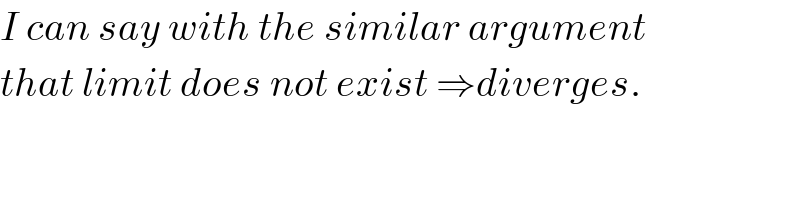
Commented by ~ À ® @ 237 ~ last updated on 06/Sep/19

A s c e r t a i n t h i s t o p r o v e t h a t t h e l i m i t e x i s t a n d i t s n u l l

- 1 ⩽ {(- 1)}^{n + 1} ⩽ 1 \Rightarrow \frac{- 1}{n^{2}} ⩽ \frac{{(- 1)}^{n + 1}}{n^{2}} ⩽ \frac{1}{n^{2}}

Commented by mathmax by abdo last updated on 06/Sep/19

\sum_{n = 1}^{\infty} \frac{{(- 1)}^{n + 1}}{n^{2}} c o n v e r g e a b s o l u t l l y d u e t o ∣ \frac{{(- 1)}^{n + 1}}{n^{2}} ∣< \frac{1}{n^{2}}

a n d Σ \frac{1}{n^{2}} c o n v e r g e s a n d \sum_{n = 1}^{\infty} \frac{{(- 1)}^{n + 1}}{l n (n)} i s a a l t e r n a t e s e r i e

a n d v e r i f y t h e c r i t e r e s o i t s c o n v e r g e s .

Commented by Learner-123 last updated on 06/Sep/19

S i r, t h e n w h y \sum_{n = 1}^{\infty} {(- 1)}^{n + 1} d i v e r g e s ?

D o e s i t f o l l o w a l t e r n a t e s e r i e ?

Commented by Prithwish sen last updated on 06/Sep/19

Actually it is an oscillating series . The value

of the sequence oscillates between 0 and 1 .

For instance take n upto 4 then the value

becomes 1 - 1 + 1 - 1 = 0 then take n = 5 the

value becomes 1 - 1 + 1 - 1 + 1 = 1 . Such a

sequences with not having fixed value are

not covergent sequence . They are oscillatory

sequence also leveled as divergent sequence .

Commented by Learner-123 last updated on 06/Sep/19

O k, t h a n k y o u a l l!

Commented by mathmax by abdo last updated on 06/Sep/19

n o s i r t h e s e q u e n c e u_{n} = {(- 1)}^{n + 1} d i v e r g e s b e c a u s e t h e e x t r a c t

s e q u e n c e d o n t g o t o t b e s a m e l i m i t l o o k

{l i m}_{n \to + \infty} u_{2 n} = - 1 a n d {l i m}_{n \to + \infty} u_{2 n + 1} = 1