Question Number 10056 by Tawakalitu ayo mi last updated on 22/Jan/17
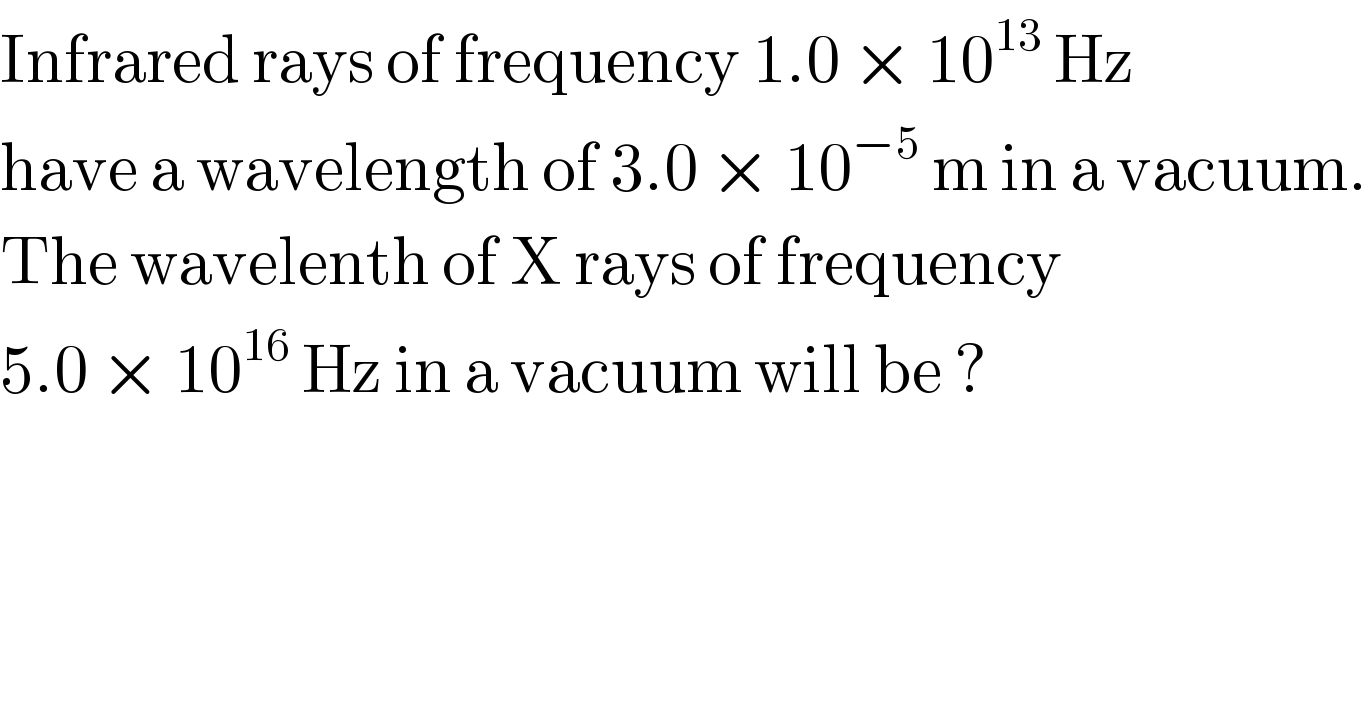
$$\mathrm{Infrared}\:\mathrm{rays}\:\mathrm{of}\:\mathrm{frequency}\:\mathrm{1}.\mathrm{0}\:×\:\mathrm{10}^{\mathrm{13}} \:\mathrm{Hz} \\ $$$$\mathrm{have}\:\mathrm{a}\:\mathrm{wavelength}\:\mathrm{of}\:\mathrm{3}.\mathrm{0}\:×\:\mathrm{10}^{−\mathrm{5}} \:\mathrm{m}\:\mathrm{in}\:\mathrm{a}\:\mathrm{vacuum}. \\ $$$$\mathrm{The}\:\mathrm{wavelenth}\:\mathrm{of}\:\mathrm{X}\:\mathrm{rays}\:\mathrm{of}\:\mathrm{frequency} \\ $$$$\mathrm{5}.\mathrm{0}\:×\:\mathrm{10}^{\mathrm{16}} \:\mathrm{Hz}\:\mathrm{in}\:\mathrm{a}\:\mathrm{vacuum}\:\mathrm{will}\:\mathrm{be}\:? \\ $$
Answered by mrW1 last updated on 22/Jan/17

$${they}\:{have}\:{the}\:{same}\:{speed}\:\left({speed}\:{of}\right. \\ $$$$\left.{light}\:\mathrm{3}×\mathrm{10}^{\mathrm{8}} \:{m}/{s}\right). \\ $$$$\lambda×\mathrm{5}.\mathrm{0}×\mathrm{10}^{\mathrm{16}} =\mathrm{3}.\mathrm{0}×\mathrm{10}^{−\mathrm{5}} ×\mathrm{1}.\mathrm{0}×\mathrm{10}^{\mathrm{13}} \\ $$$$\lambda=\frac{\mathrm{3}.\mathrm{0}×\mathrm{10}^{−\mathrm{5}} ×\mathrm{1}.\mathrm{0}×\mathrm{10}^{\mathrm{13}} }{\mathrm{5}.\mathrm{0}×\mathrm{10}^{\mathrm{16}} }=\mathrm{6}.\mathrm{0}×\mathrm{10}^{−\mathrm{9}} \:{m} \\ $$
Commented by Tawakalitu ayo mi last updated on 22/Jan/17
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
