Question Number 67246 by Learner-123 last updated on 24/Aug/19
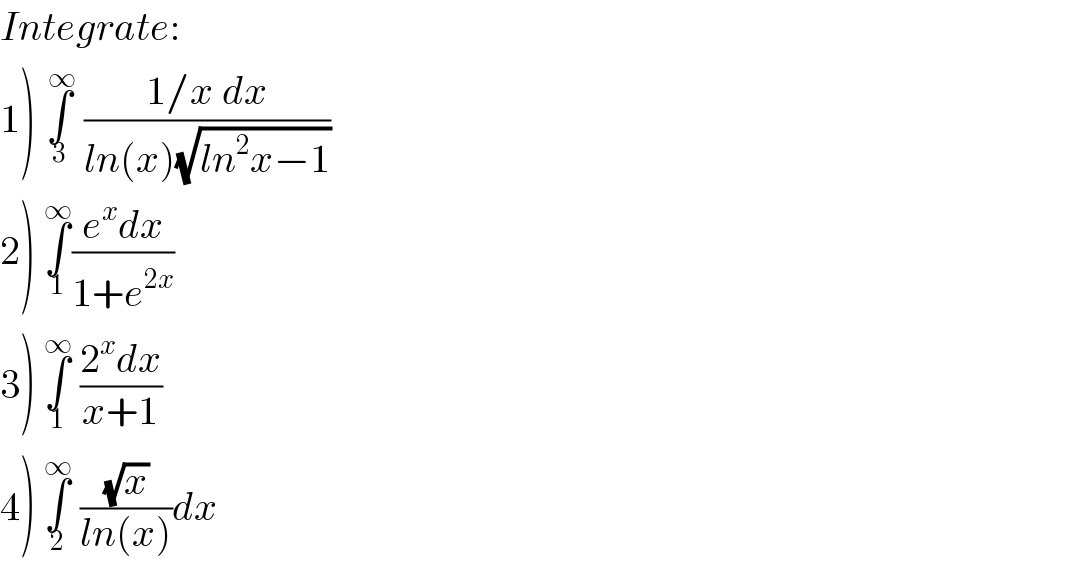
$${Integrate}: \\ $$$$\left.\mathrm{1}\right)\:\underset{\mathrm{3}} {\overset{\:\infty} {\int}}\:\frac{\mathrm{1}/{x}\:{dx}}{{ln}\left({x}\right)\sqrt{{ln}^{\mathrm{2}} {x}−\mathrm{1}}} \\ $$$$\left.\mathrm{2}\right)\:\underset{\mathrm{1}} {\overset{\infty} {\int}}\frac{{e}^{{x}} {dx}}{\mathrm{1}+{e}^{\mathrm{2}{x}} } \\ $$$$\left.\mathrm{3}\right)\:\underset{\mathrm{1}} {\overset{\infty} {\int}}\:\frac{\mathrm{2}^{{x}} {dx}}{{x}+\mathrm{1}} \\ $$$$\left.\mathrm{4}\right)\:\underset{\mathrm{2}} {\overset{\infty} {\int}}\:\frac{\sqrt{{x}}}{{ln}\left({x}\right)}{dx} \\ $$
Commented by MJS last updated on 24/Aug/19

$$\left.\mathrm{3}\left.\right)\:\mathrm{and}\:\mathrm{4}\right)\:\mathrm{are}\:\mathrm{not}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{with} \\ $$$$\mathrm{elementary}\:\mathrm{functions}… \\ $$
Commented by mathmax by abdo last updated on 24/Aug/19
![2) let I =∫_1 ^∞ (e^x /(1+e^(2x) ))dx changement e^x =t give I =∫_e ^(+∞) (t/(1+t^2 ))(dt/t) =∫_e ^(+∞) (dt/(1+t^2 )) =[arctan(t)]_e ^(+∞) =(π/2) −arctan(e).](https://www.tinkutara.com/question/Q67251.png)
$$\left.\mathrm{2}\right)\:{let}\:{I}\:=\int_{\mathrm{1}} ^{\infty} \:\frac{{e}^{{x}} }{\mathrm{1}+{e}^{\mathrm{2}{x}} }{dx}\:\:\:{changement}\:{e}^{{x}} \:={t}\:{give} \\ $$$${I}\:=\int_{{e}} ^{+\infty} \:\frac{{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\frac{{dt}}{{t}}\:=\int_{{e}} ^{+\infty} \:\frac{{dt}}{\mathrm{1}+{t}^{\mathrm{2}} }\:=\left[{arctan}\left({t}\right)\right]_{{e}} ^{+\infty} \:=\frac{\pi}{\mathrm{2}}\:−{arctan}\left({e}\right). \\ $$
Commented by mathmax by abdo last updated on 24/Aug/19
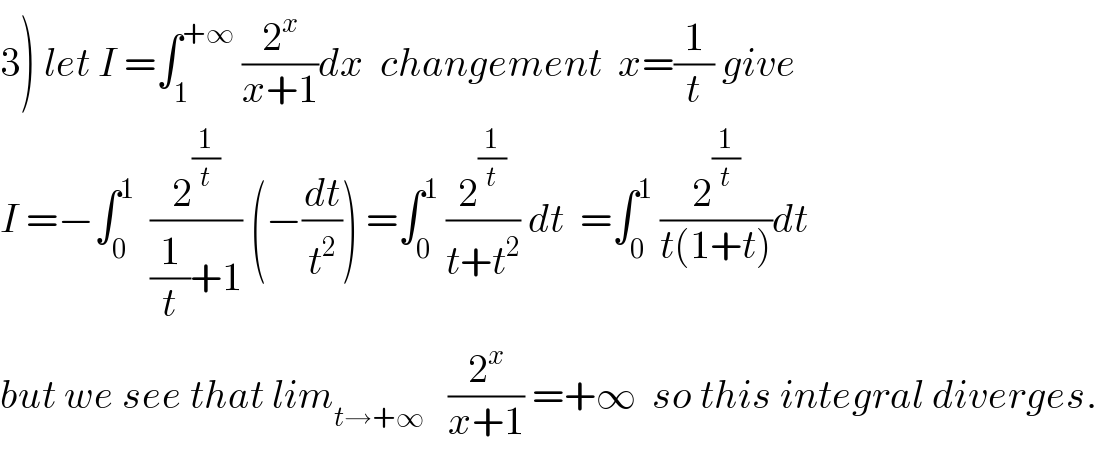
$$\left.\mathrm{3}\right)\:{let}\:{I}\:=\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{2}^{{x}} }{{x}+\mathrm{1}}{dx}\:\:{changement}\:\:{x}=\frac{\mathrm{1}}{{t}}\:{give} \\ $$$${I}\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{\mathrm{2}^{\frac{\mathrm{1}}{{t}}} }{\frac{\mathrm{1}}{{t}}+\mathrm{1}}\:\left(−\frac{{dt}}{{t}^{\mathrm{2}} }\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}^{\frac{\mathrm{1}}{{t}}} }{{t}+{t}^{\mathrm{2}} }\:{dt}\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{2}^{\frac{\mathrm{1}}{{t}}} }{{t}\left(\mathrm{1}+{t}\right)}{dt} \\ $$$${but}\:{we}\:{see}\:{that}\:{lim}_{{t}\rightarrow+\infty} \:\:\:\frac{\mathrm{2}^{{x}} }{{x}+\mathrm{1}}\:=+\infty\:\:{so}\:{this}\:{integral}\:{diverges}. \\ $$
Commented by mathmax by abdo last updated on 24/Aug/19
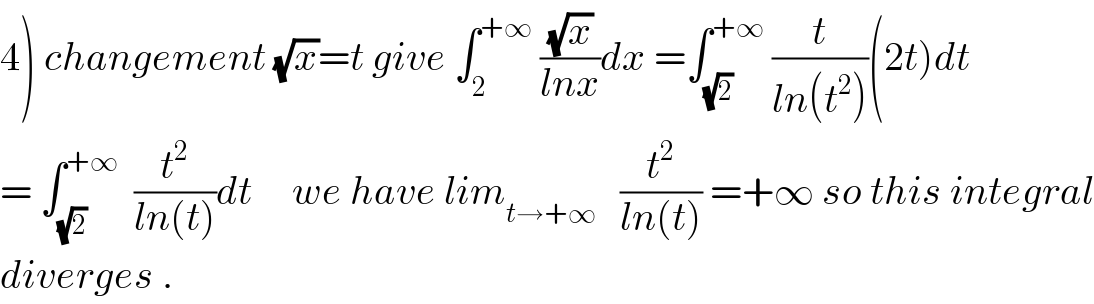
$$\left.\mathrm{4}\right)\:{changement}\:\sqrt{{x}}={t}\:{give}\:\int_{\mathrm{2}} ^{+\infty} \:\frac{\sqrt{{x}}}{{lnx}}{dx}\:=\int_{\sqrt{\mathrm{2}}} ^{+\infty} \:\frac{{t}}{{ln}\left({t}^{\mathrm{2}} \right)}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\:\int_{\sqrt{\mathrm{2}}} ^{+\infty} \:\:\frac{{t}^{\mathrm{2}} }{{ln}\left({t}\right)}{dt}\:\:\:\:\:{we}\:{have}\:{lim}_{{t}\rightarrow+\infty} \:\:\:\frac{{t}^{\mathrm{2}} }{{ln}\left({t}\right)}\:=+\infty\:{so}\:{this}\:{integral} \\ $$$${diverges}\:. \\ $$
Answered by MJS last updated on 24/Aug/19
![1) ∫(((1/x)dx)/(ln x (√(ln^2 x −1))))= [t=ln x → dx=xdt] =∫(dt/(t(√(t^2 −1))))= [u=(√(t^2 −1)) → dt=((√(t^2 −1))/t)du] =∫(du/(u^2 +1))=arctan u =arctan (√(t^2 −1)) =arctan (√(ln^2 x −1)) +C](https://www.tinkutara.com/question/Q67247.png)
$$\left.\mathrm{1}\right) \\ $$$$\int\frac{\frac{\mathrm{1}}{{x}}{dx}}{\mathrm{ln}\:{x}\:\sqrt{\mathrm{ln}^{\mathrm{2}} \:{x}\:−\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{ln}\:{x}\:\rightarrow\:{dx}={xdt}\right] \\ $$$$=\int\frac{{dt}}{{t}\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{u}=\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}\:\rightarrow\:{dt}=\frac{\sqrt{{t}^{\mathrm{2}} −\mathrm{1}}}{{t}}{du}\right] \\ $$$$=\int\frac{{du}}{{u}^{\mathrm{2}} +\mathrm{1}}=\mathrm{arctan}\:{u}\:=\mathrm{arctan}\:\sqrt{\mathrm{t}^{\mathrm{2}} −\mathrm{1}}\:=\mathrm{arctan}\:\sqrt{\mathrm{ln}^{\mathrm{2}} \:{x}\:−\mathrm{1}}\:+{C} \\ $$
Commented by MJS last updated on 24/Aug/19
![in one step: ∫(((1/x)dx)/(ln x (√(ln^2 x −1))))= [t=(√(ln^2 x −1)) → dx=((x(√(ln^2 x −1)))/(ln x))] =∫(dt/(t^2 +1))=...](https://www.tinkutara.com/question/Q67248.png)
$$\mathrm{in}\:\mathrm{one}\:\mathrm{step}: \\ $$$$\int\frac{\frac{\mathrm{1}}{{x}}{dx}}{\mathrm{ln}\:{x}\:\sqrt{\mathrm{ln}^{\mathrm{2}} \:{x}\:−\mathrm{1}}}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\mathrm{ln}^{\mathrm{2}} \:{x}\:−\mathrm{1}}\:\rightarrow\:{dx}=\frac{{x}\sqrt{\mathrm{ln}^{\mathrm{2}} \:{x}\:−\mathrm{1}}}{\mathrm{ln}\:{x}}\right] \\ $$$$=\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=… \\ $$
Commented by Learner-123 last updated on 25/Aug/19

$${thank}\:{you}\:{sir}. \\ $$
Answered by MJS last updated on 24/Aug/19
![2) ∫(e^x /(1+e^(2x) ))dx= [t=e^x → dx=(dt/e^x )] =∫(dt/(t^2 +1))=arctan t =arctan e^x +C](https://www.tinkutara.com/question/Q67249.png)
$$\left.\mathrm{2}\right) \\ $$$$\int\frac{\mathrm{e}^{{x}} }{\mathrm{1}+\mathrm{e}^{\mathrm{2}{x}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{e}^{{x}} \:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{e}^{{x}} }\right] \\ $$$$=\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}=\mathrm{arctan}\:{t}\:=\mathrm{arctan}\:\mathrm{e}^{{x}} \:+{C} \\ $$
