Question Number 7326 by sou1618 last updated on 23/Aug/16
![Is it correct? floor(x)=⌊x⌋=[x] floor(x)={n ∣ n∈Z , x−1<n≤x} e.g.... floor(3)=3 floor(3.4)=3 floor(−2.5)=−3 floor(−π)=−4](https://www.tinkutara.com/question/Q7326.png)
$${Is}\:{it}\:{correct}? \\ $$$$\:\:{floor}\left({x}\right)=\lfloor{x}\rfloor=\left[{x}\right] \\ $$$$ \\ $$$$ \\ $$$${floor}\left({x}\right)=\left\{{n}\:\mid\:{n}\in\mathbb{Z}\:,\:{x}−\mathrm{1}<{n}\leqslant{x}\right\} \\ $$$${e}.{g}…. \\ $$$${floor}\left(\mathrm{3}\right)=\mathrm{3} \\ $$$${floor}\left(\mathrm{3}.\mathrm{4}\right)=\mathrm{3} \\ $$$${floor}\left(−\mathrm{2}.\mathrm{5}\right)=−\mathrm{3} \\ $$$${floor}\left(−\pi\right)=−\mathrm{4} \\ $$
Commented by Yozzia last updated on 24/Aug/16
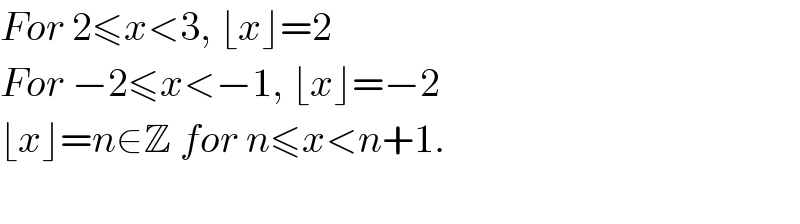
$${For}\:\mathrm{2}\leqslant{x}<\mathrm{3},\:\lfloor{x}\rfloor=\mathrm{2}\: \\ $$$${For}\:−\mathrm{2}\leqslant{x}<−\mathrm{1},\:\lfloor{x}\rfloor=−\mathrm{2} \\ $$$$\lfloor{x}\rfloor={n}\in\mathbb{Z}\:{for}\:{n}\leqslant{x}<{n}+\mathrm{1}. \\ $$$$ \\ $$
Commented by sou1618 last updated on 24/Aug/16

$${thanks} \\ $$
