Menu Close

Is-the-section-marked-correct-i-1-x-i-x-n-1-x-i-1-n-i-1-2-x-1-1-2-1-2-3-1-2-x-1-x-2-x-1-3-x-2-x-1-2-x-1-m-1-x-n-1-m-i-1-

Tinku Tara 0 Comments
Pin




Question Number 4639 by FilupSmith last updated on 17/Feb/16
Is the section marked (∗) correct? Π_(i=1) ^x i=x! Π_(n=1) ^x (Π_(i=1) ^n i)=1!×2!×...×x! =1×(1×2)×(1×2×3)×...×(1×2×...×x) =1^x 2^(x−1) 3^(x−2) ...(x−1)^2 x^1 (∗) Π_(m=1) ^x (Π_(n=1) ^m (Π_(i=1) ^n i))=Π_(m=1) ^x (1^m 2^(m−1) ...(m−1)^2 m) =1×(1^2 2^1 )×(1^3 2^2 3^1 )×(1^4 2^3 3^2 4^1 )×...×(1^x 2^(x−1) ...x^1 ) =1^(Σ_(i=x−0) ^x i) ×2^(Σ_(i=x−1) ^x i) ×3^(Σ_(i=x−2) ^x i) ×...(x−1)^(Σ_(i=x−(x−1)+1) ^x i) ×x^(Σ_(i=x−x+1) ^x i) =Π_(i=1) ^x (i^((Σ_(k=x−i+1) ^x k)) ) =Π_(i=1) ^x i^((1/2)x(2x−i+1)) =Π_(i=1) ^x i^(x^2 +(1/2)(1−i)) =Π_(i=1) ^x i^((x^2 )) (√i^(1−i) ) ∴ Π_(m=1) ^x (Π_(n=1) ^m (Π_(i=1) ^n i))=Π_(i=1) ^x i^((1/2)x(2x−i+1))
$$\mathrm{Is}\:\mathrm{the}\:\mathrm{section}\:\mathrm{marked}\:\left(\ast\right)\:{correct}? \\ $$$$ \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i}={x}! \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{{x}} {\prod}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{i}\right)=\mathrm{1}!×\mathrm{2}!×…×{x}! \\ $$$$=\mathrm{1}×\left(\mathrm{1}×\mathrm{2}\right)×\left(\mathrm{1}×\mathrm{2}×\mathrm{3}\right)×…×\left(\mathrm{1}×\mathrm{2}×…×{x}\right) \\ $$$$=\mathrm{1}^{{x}} \mathrm{2}^{{x}−\mathrm{1}} \mathrm{3}^{{x}−\mathrm{2}} …\left({x}−\mathrm{1}\right)^{\mathrm{2}} {x}^{\mathrm{1}} \\ $$$$ \\ $$$$\left(\ast\right) \\ $$$$\underset{{m}=\mathrm{1}} {\overset{{x}} {\prod}}\left(\underset{{n}=\mathrm{1}} {\overset{{m}} {\prod}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{i}\right)\right)=\underset{{m}=\mathrm{1}} {\overset{{x}} {\prod}}\left(\mathrm{1}^{{m}} \mathrm{2}^{{m}−\mathrm{1}} …\left({m}−\mathrm{1}\right)^{\mathrm{2}} {m}\right) \\ $$$$=\mathrm{1}×\left(\mathrm{1}^{\mathrm{2}} \mathrm{2}^{\mathrm{1}} \right)×\left(\mathrm{1}^{\mathrm{3}} \mathrm{2}^{\mathrm{2}} \mathrm{3}^{\mathrm{1}} \right)×\left(\mathrm{1}^{\mathrm{4}} \mathrm{2}^{\mathrm{3}} \mathrm{3}^{\mathrm{2}} \mathrm{4}^{\mathrm{1}} \right)×…×\left(\mathrm{1}^{{x}} \mathrm{2}^{{x}−\mathrm{1}} …{x}^{\mathrm{1}} \right) \\ $$$$=\mathrm{1}^{\underset{{i}={x}−\mathrm{0}} {\overset{{x}} {\sum}}{i}} ×\mathrm{2}^{\underset{{i}={x}−\mathrm{1}} {\overset{{x}} {\sum}}{i}} ×\mathrm{3}^{\underset{{i}={x}−\mathrm{2}} {\overset{{x}} {\sum}}{i}} ×…\left({x}−\mathrm{1}\right)^{\underset{{i}={x}−\left({x}−\mathrm{1}\right)+\mathrm{1}} {\overset{{x}} {\sum}}{i}} ×{x}^{\underset{{i}={x}−{x}+\mathrm{1}} {\overset{{x}} {\sum}}{i}} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}\left({i}^{\left(\underset{{k}={x}−{i}+\mathrm{1}} {\overset{{x}} {\sum}}{k}\right)} \right) \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i}^{\frac{\mathrm{1}}{\mathrm{2}}{x}\left(\mathrm{2}{x}−{i}+\mathrm{1}\right)} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i}^{{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−{i}\right)} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i}^{\left({x}^{\mathrm{2}} \right)} \sqrt{{i}^{\mathrm{1}−{i}} } \\ $$$$ \\ $$$$\therefore\:\underset{{m}=\mathrm{1}} {\overset{{x}} {\prod}}\left(\underset{{n}=\mathrm{1}} {\overset{{m}} {\prod}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{i}\right)\right)=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i}^{\frac{\mathrm{1}}{\mathrm{2}}{x}\left(\mathrm{2}{x}−{i}+\mathrm{1}\right)} \\ $$
Commented by Yozzii last updated on 17/Feb/16
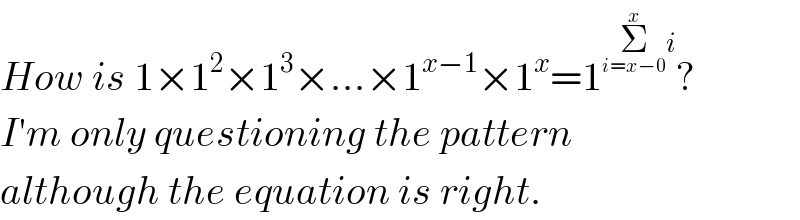
How is 1×1^2 ×1^3 ×...×1^(x−1) ×1^x =1^(Σ_(i=x−0) ^x i) ? I′m only questioning the pattern although the equation is right.
$${How}\:{is}\:\mathrm{1}×\mathrm{1}^{\mathrm{2}} ×\mathrm{1}^{\mathrm{3}} ×…×\mathrm{1}^{{x}−\mathrm{1}} ×\mathrm{1}^{{x}} =\mathrm{1}^{\underset{{i}={x}−\mathrm{0}} {\overset{{x}} {\sum}}{i}} ? \\ $$$${I}'{m}\:{only}\:{questioning}\:{the}\:{pattern} \\ $$$${although}\:{the}\:{equation}\:{is}\:{right}. \\ $$
Commented by FilupSmith last updated on 18/Feb/16
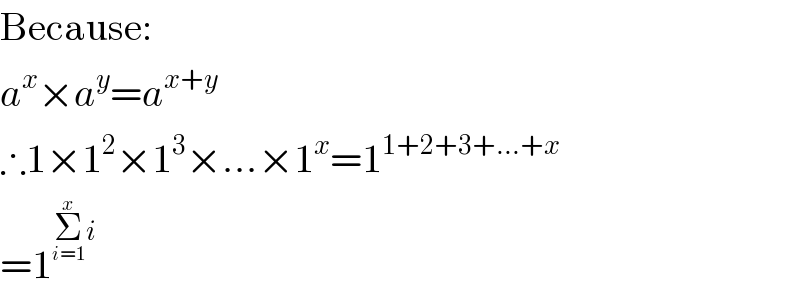
Because: a^x ×a^y =a^(x+y) ∴1×1^2 ×1^3 ×...×1^x =1^(1+2+3+...+x) =1^(Σ_(i=1) ^x i)
$$\mathrm{Because}: \\ $$$${a}^{{x}} ×{a}^{{y}} ={a}^{{x}+{y}} \\ $$$$\therefore\mathrm{1}×\mathrm{1}^{\mathrm{2}} ×\mathrm{1}^{\mathrm{3}} ×…×\mathrm{1}^{{x}} =\mathrm{1}^{\mathrm{1}+\mathrm{2}+\mathrm{3}+…+{x}} \\ $$$$=\mathrm{1}^{\underset{{i}=\mathrm{1}} {\overset{{x}} {\sum}}{i}} \\ $$
Commented by FilupSmith last updated on 18/Feb/16
1×(1^2 2^1 )×(1^3 2^2 3^1 )×(1^4 2^3 3^2 4^1 )×...×(1^x 2^(x−1) ...x^1 ) =(1×1^2 ×...1^x )×(2^2 ×...×2^x )×(3^3 ×...×3^x )... for 1^(Σ_(k=1) ^x k) =1^1 =1^(Σ_(k=1) ^x k) =1^(Σ_(k=1) ^x k) for 2^(Σ_(k=2) ^x k) =2^(Σ_(k=2) ^x k) =2^(2+3+...+x) But... Π_(m=1) ^x (Π_(n=1) ^m (Π_(i=1) ^n i)) The red part changes the value for x for each section: 1_(x=1) ×(1^2 2^1 )_(x=2) ×(1^3 2^2 3^3 )_(x=3) ×...×(1^x 2^(x−1) ...x)_(x=x)
$$\mathrm{1}×\left(\mathrm{1}^{\mathrm{2}} \mathrm{2}^{\mathrm{1}} \right)×\left(\mathrm{1}^{\mathrm{3}} \mathrm{2}^{\mathrm{2}} \mathrm{3}^{\mathrm{1}} \right)×\left(\mathrm{1}^{\mathrm{4}} \mathrm{2}^{\mathrm{3}} \mathrm{3}^{\mathrm{2}} \mathrm{4}^{\mathrm{1}} \right)×…×\left(\mathrm{1}^{{x}} \mathrm{2}^{{x}−\mathrm{1}} …{x}^{\mathrm{1}} \right) \\ $$$$=\left(\mathrm{1}×\mathrm{1}^{\mathrm{2}} ×…\mathrm{1}^{{x}} \right)×\left(\mathrm{2}^{\mathrm{2}} ×…×\mathrm{2}^{{x}} \right)×\left(\mathrm{3}^{\mathrm{3}} ×…×\mathrm{3}^{{x}} \right)… \\ $$$$ \\ $$$${for}\:\mathrm{1}^{\underset{{k}=\mathrm{1}} {\overset{{x}} {\sum}}{k}} =\mathrm{1}^{\mathrm{1}} =\mathrm{1}^{\underset{{k}=\mathrm{1}} {\overset{{x}} {\sum}}{k}} =\mathrm{1}^{\underset{{k}=\mathrm{1}} {\overset{{x}} {\sum}}{k}} \\ $$$${for}\:\mathrm{2}^{\underset{{k}=\mathrm{2}} {\overset{{x}} {\sum}}{k}} =\mathrm{2}^{\underset{{k}=\mathrm{2}} {\overset{{x}} {\sum}}{k}} =\mathrm{2}^{\mathrm{2}+\mathrm{3}+…+{x}} \\ $$$$ \\ $$$$\mathrm{But}… \\ $$$$\underset{{m}=\mathrm{1}} {\overset{{x}} {\prod}}\left(\underset{{n}=\mathrm{1}} {\overset{{m}} {\prod}}\left(\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}{i}\right)\right)\:\mathrm{The}\:\mathrm{red}\:\mathrm{part}\:\mathrm{changes}\:\mathrm{the} \\ $$$$\mathrm{value}\:\mathrm{for}\:{x}\:\mathrm{for}\:\mathrm{each}\:\mathrm{section}: \\ $$$$\underset{{x}=\mathrm{1}} {\mathrm{1}}×\underset{{x}=\mathrm{2}} {\left(\mathrm{1}^{\mathrm{2}} \mathrm{2}^{\mathrm{1}} \right)}×\underset{{x}=\mathrm{3}} {\left(\mathrm{1}^{\mathrm{3}} \mathrm{2}^{\mathrm{2}} \mathrm{3}^{\mathrm{3}} \right)}×…×\underset{{x}={x}} {\left(\mathrm{1}^{{x}} \mathrm{2}^{{x}−\mathrm{1}} …{x}\right)} \\ $$
Commented by FilupSmith last updated on 18/Feb/16
i was tired when i wrote this post so i dont remember my logic
$$\mathrm{i}\:\mathrm{was}\:\mathrm{tired}\:\mathrm{when}\:\mathrm{i}\:\mathrm{wrote}\:\mathrm{this}\:\mathrm{post} \\ $$$$\mathrm{so}\:\mathrm{i}\:\mathrm{dont}\:\mathrm{remember}\:\mathrm{my}\:\mathrm{logic} \\ $$
Commented by FilupSmith last updated on 18/Feb/16
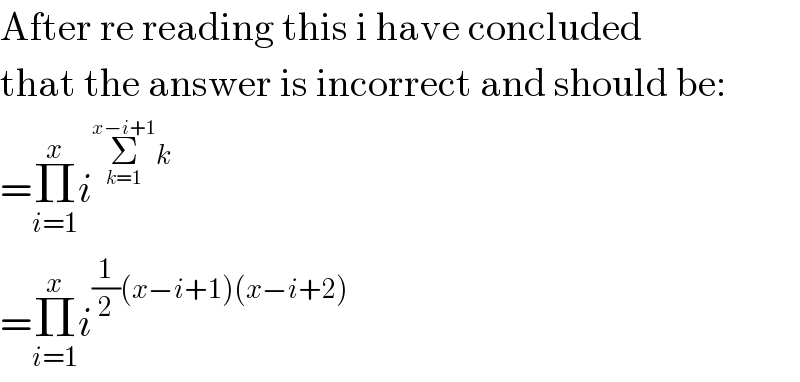
After re reading this i have concluded that the answer is incorrect and should be: =Π_(i=1) ^x i^(Σ_(k=1) ^(x−i+1) k) =Π_(i=1) ^x i^((1/2)(x−i+1)(x−i+2))
$$\mathrm{After}\:\mathrm{re}\:\mathrm{reading}\:\mathrm{this}\:\mathrm{i}\:\mathrm{have}\:\mathrm{concluded} \\ $$$$\mathrm{that}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{incorrect}\:\mathrm{and}\:\mathrm{should}\:\mathrm{be}: \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i}^{\underset{{k}=\mathrm{1}} {\overset{{x}−{i}+\mathrm{1}} {\sum}}{k}} \\ $$$$=\underset{{i}=\mathrm{1}} {\overset{{x}} {\prod}}{i}^{\frac{\mathrm{1}}{\mathrm{2}}\left({x}−{i}+\mathrm{1}\right)\left({x}−{i}+\mathrm{2}\right)} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *