Is-there-a-way-to-evaluate-the-following-S-2-2-2-2-2-

Question Number 2275 by Filup last updated on 13/Nov/15

Is there a way to evaluate the following :

S = 2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \dots}}}}

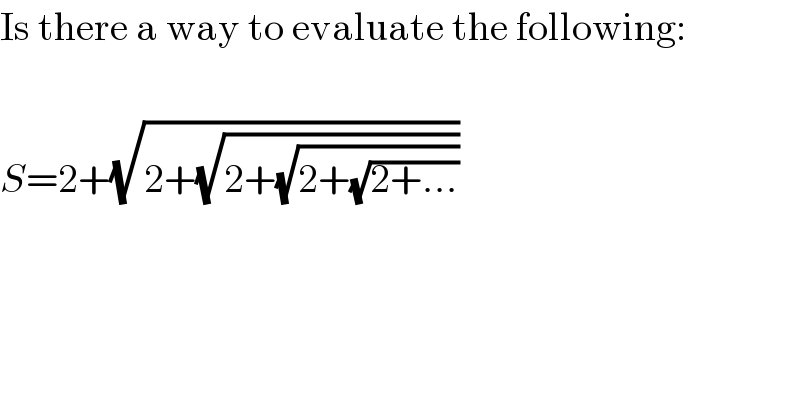
Answered by Rasheed Soomro last updated on 13/Nov/15

S = 2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \dots}}}}

{(S - 2)}^{2} = {(\sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \dots}}}})}^{2}

S^{2} - 4 S + 4 = 2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \dots}}}}

= S

S^{2} - 5 S + 4 = 0

(S - 1) (S - 4) = 0

S = 1 ∣ S = 4

S i n c e w e h a v e s q u a r e d b o t h s i d e s t h e r e s u l t i n g e q u a t i o n

i s n o t c o m p l e t e l y e q u i v a l e n t t o t h e o r i g i n a l a n d t h e r e

i s p o s s i b i l i t y o f e x t r a n e o u s r o o t s .

C l e a r l y S > 2 b e c a u s e \sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \dots}}}} i s p o s i t v e .

H e n c e S = 1 i s e x t r a n e o u s r o o t a n d

S = 4 i s r e q u i r e d s u m .

Commented by Filup last updated on 13/Nov/15

A M A Z I N G! I am honestly fascinated!

Commented by Filup last updated on 13/Nov/15

So how can we be sure S > 2

I {can}^{'} t see how, because \sqrt{x} ⩽ x

So, if : 2 + \sqrt{2 + \sqrt{\dots}} is small,

\sqrt{2 + \sqrt{2 + \sqrt{\dots}}} is smaller

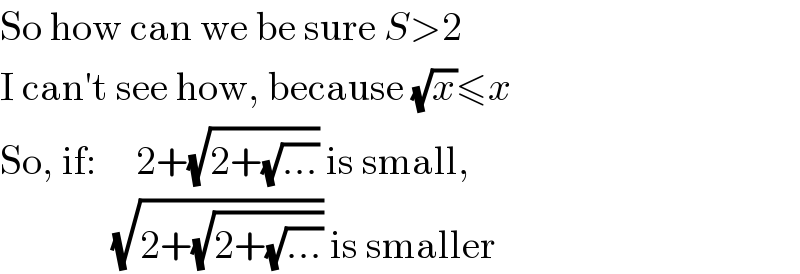
Commented by RasheedAhmad last updated on 13/Nov/15

S = 2 + \underset{- - - - - - - - - - - - - - -}{\sqrt{2 + \sqrt{2 + \sqrt{2 + \sqrt{2 + \dots}}}}} [G i v e n]

U n d e r l i n e d e x p r e s s i o n > 0

∴ S = 2 + p o s i t i v e n u m b e r

∴ S > 2

Commented by Filup last updated on 14/Nov/15

ahh i must of had a massive brain fart

Facebook Tweet Pin