Question Number 4132 by prakash jain last updated on 29/Dec/15
![Is there f(n) such that lim_(x→0) [Σ_(n=1) ^∞ f(n)x^n ]≠0 f(n) is independent of x.](https://www.tinkutara.com/question/Q4132.png)
$$\mathrm{Is}\:\mathrm{there}\:{f}\left({n}\right)\:\mathrm{such}\:\mathrm{that} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left[\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\:{f}\left({n}\right){x}^{{n}} \right]\neq\mathrm{0} \\ $$$${f}\left({n}\right)\:\mathrm{is}\:\mathrm{independent}\:\mathrm{of}\:{x}. \\ $$
Commented by Yozzii last updated on 29/Dec/15
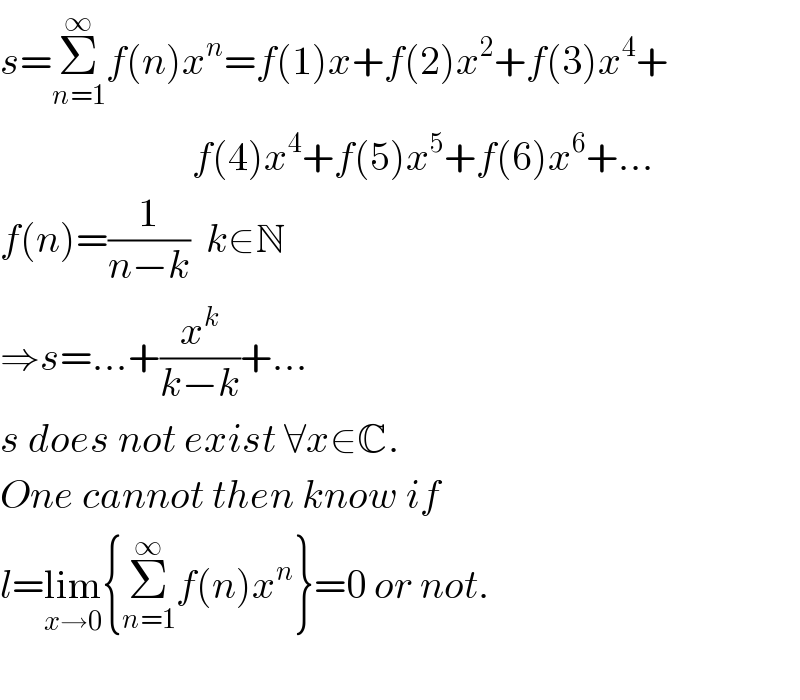
$${s}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{f}\left({n}\right){x}^{{n}} ={f}\left(\mathrm{1}\right){x}+{f}\left(\mathrm{2}\right){x}^{\mathrm{2}} +{f}\left(\mathrm{3}\right){x}^{\mathrm{4}} + \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\mathrm{4}\right){x}^{\mathrm{4}} +{f}\left(\mathrm{5}\right){x}^{\mathrm{5}} +{f}\left(\mathrm{6}\right){x}^{\mathrm{6}} +… \\ $$$${f}\left({n}\right)=\frac{\mathrm{1}}{{n}−{k}}\:\:{k}\in\mathbb{N} \\ $$$$\Rightarrow{s}=…+\frac{{x}^{{k}} }{{k}−{k}}+… \\ $$$${s}\:{does}\:{not}\:{exist}\:\forall{x}\in\mathbb{C}. \\ $$$${One}\:{cannot}\:{then}\:{know}\:{if} \\ $$$${l}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left\{\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{f}\left({n}\right){x}^{{n}} \right\}=\mathrm{0}\:{or}\:{not}. \\ $$$$ \\ $$
