Question Number 1050 by tera last updated on 23/May/15
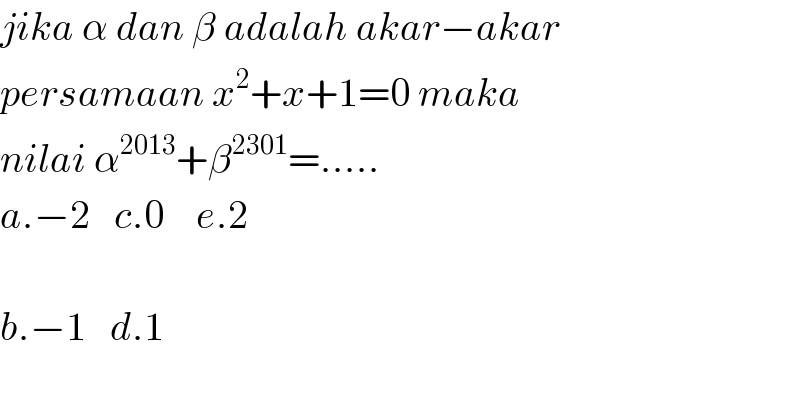
$${jika}\:\alpha\:{dan}\:\beta\:{adalah}\:{akar}−{akar} \\ $$$${persamaan}\:{x}^{\mathrm{2}} +{x}+\mathrm{1}=\mathrm{0}\:{maka}\: \\ $$$${nilai}\:\alpha^{\mathrm{2013}} +\beta^{\mathrm{2301}} =….. \\ $$$${a}.−\mathrm{2}\:\:\:{c}.\mathrm{0}\:\:\:\:{e}.\mathrm{2} \\ $$$$ \\ $$$${b}.−\mathrm{1}\:\:\:{d}.\mathrm{1} \\ $$
Answered by prakash jain last updated on 23/May/15
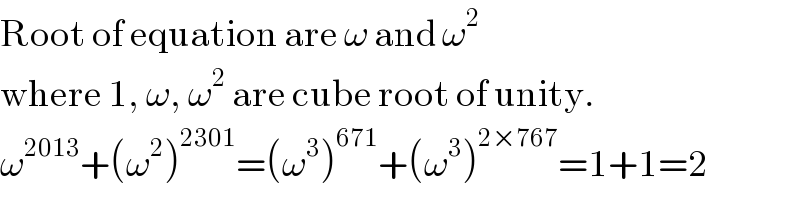
$$\mathrm{Root}\:\mathrm{of}\:\mathrm{equation}\:\mathrm{are}\:\omega\:\mathrm{and}\:\omega^{\mathrm{2}} \\ $$$$\mathrm{where}\:\mathrm{1},\:\omega,\:\omega^{\mathrm{2}} \:\mathrm{are}\:\mathrm{cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{unity}. \\ $$$$\omega^{\mathrm{2013}} +\left(\omega^{\mathrm{2}} \right)^{\mathrm{2301}} =\left(\omega^{\mathrm{3}} \right)^{\mathrm{671}} +\left(\omega^{\mathrm{3}} \right)^{\mathrm{2}×\mathrm{767}} =\mathrm{1}+\mathrm{1}=\mathrm{2} \\ $$
Commented by prakash jain last updated on 23/May/15
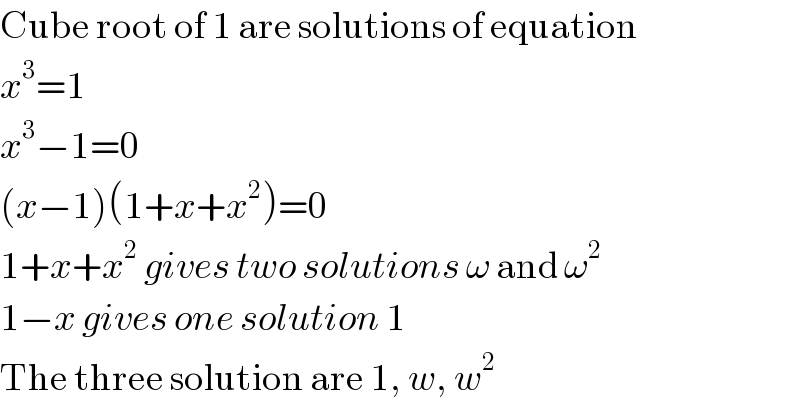
$$\mathrm{Cube}\:\mathrm{root}\:\mathrm{of}\:\mathrm{1}\:\mathrm{are}\:\mathrm{solutions}\:\mathrm{of}\:\mathrm{equation} \\ $$$${x}^{\mathrm{3}} =\mathrm{1} \\ $$$${x}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\mathrm{1}+{x}+{x}^{\mathrm{2}} \:{gives}\:{two}\:{solutions}\:\omega\:\mathrm{and}\:\omega^{\mathrm{2}} \\ $$$$\mathrm{1}−{x}\:{gives}\:{one}\:{solution}\:\mathrm{1} \\ $$$$\mathrm{The}\:\mathrm{three}\:\mathrm{solution}\:\mathrm{are}\:\mathrm{1},\:{w},\:{w}^{\mathrm{2}} \\ $$
