Question Number 140750 by SOMEDAVONG last updated on 12/May/21

$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{cos}^{\mathrm{3}} \mathrm{k}=? \\ $$
Answered by Dwaipayan Shikari last updated on 12/May/21
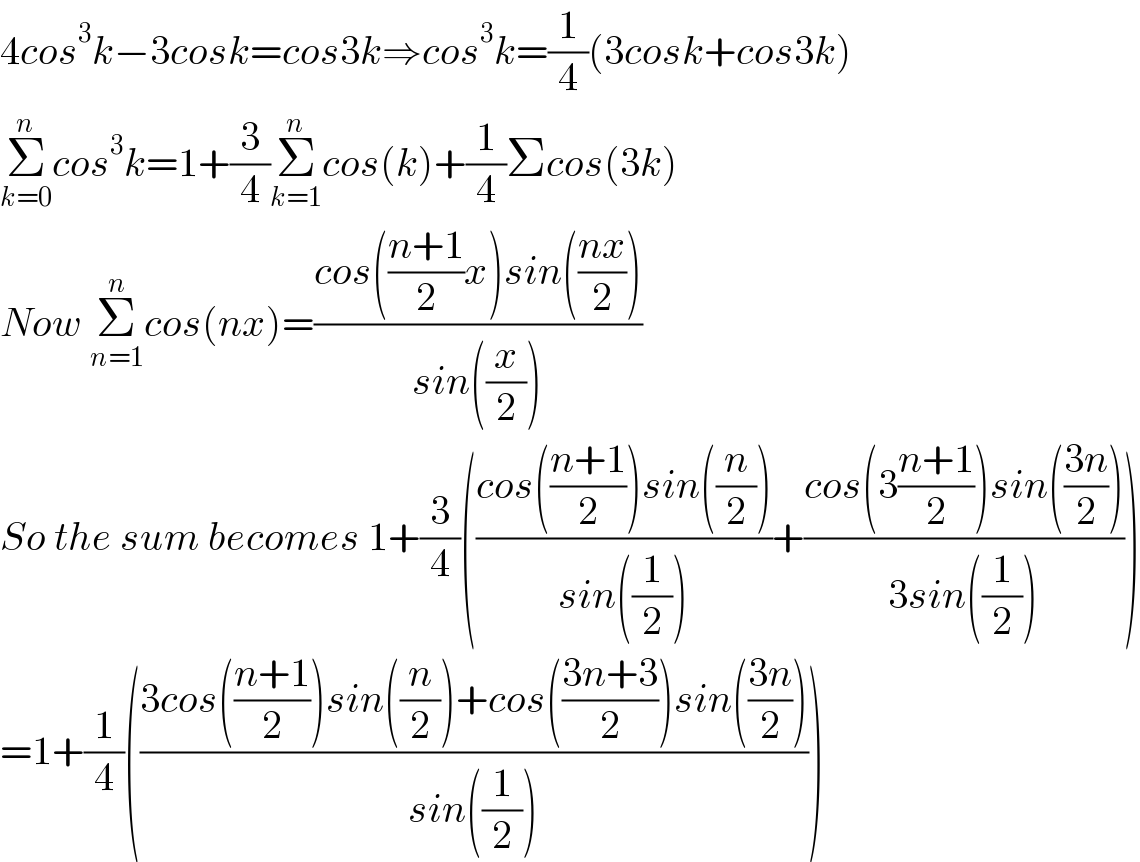
$$\mathrm{4}{cos}^{\mathrm{3}} {k}−\mathrm{3}{cosk}={cos}\mathrm{3}{k}\Rightarrow{cos}^{\mathrm{3}} {k}=\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{3}{cosk}+{cos}\mathrm{3}{k}\right) \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{cos}^{\mathrm{3}} {k}=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{cos}\left({k}\right)+\frac{\mathrm{1}}{\mathrm{4}}\Sigma{cos}\left(\mathrm{3}{k}\right) \\ $$$${Now}\:\underset{{n}=\mathrm{1}} {\overset{{n}} {\sum}}{cos}\left({nx}\right)=\frac{{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}{x}\right){sin}\left(\frac{{nx}}{\mathrm{2}}\right)}{{sin}\left(\frac{{x}}{\mathrm{2}}\right)}\: \\ $$$${So}\:{the}\:{sum}\:{becomes}\:\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right){sin}\left(\frac{{n}}{\mathrm{2}}\right)}{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}+\frac{{cos}\left(\mathrm{3}\frac{{n}+\mathrm{1}}{\mathrm{2}}\right){sin}\left(\frac{\mathrm{3}{n}}{\mathrm{2}}\right)}{\mathrm{3}{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\right) \\ $$$$=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{3}{cos}\left(\frac{{n}+\mathrm{1}}{\mathrm{2}}\right){sin}\left(\frac{{n}}{\mathrm{2}}\right)+{cos}\left(\frac{\mathrm{3}{n}+\mathrm{3}}{\mathrm{2}}\right){sin}\left(\frac{\mathrm{3}{n}}{\mathrm{2}}\right)}{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}\right) \\ $$
