Question Number 72483 by TawaTawa last updated on 29/Oct/19
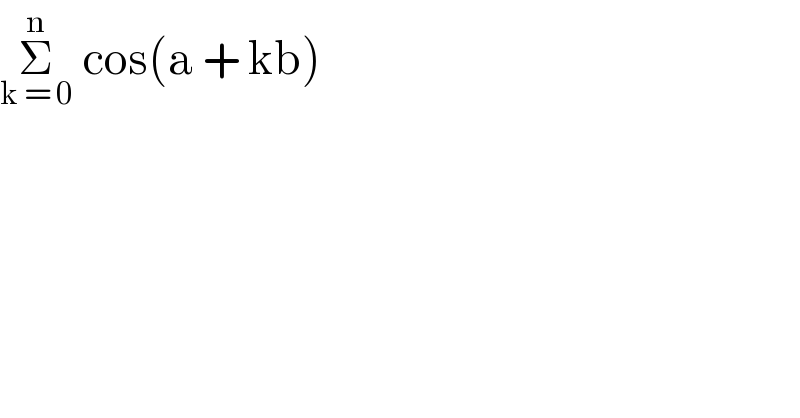
$$\underset{\mathrm{k}\:=\:\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\:\mathrm{cos}\left(\mathrm{a}\:+\:\mathrm{kb}\right) \\ $$
Answered by Tanmay chaudhury last updated on 29/Oct/19

$${T}_{{k}} ={cos}\left({a}+{kb}\right) \\ $$$${S}={T}_{\mathrm{0}} +{T}_{\mathrm{1}} +{T}_{\mathrm{2}} +…+{T}_{{n}} \\ $$$${T}_{\mathrm{0}} ×\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}=\mathrm{2}{cosa}×{sin}\frac{{b}}{\mathrm{2}}={sin}\left({a}+\frac{{b}}{\mathrm{2}}\right)−{sin}\left({a}−\frac{{b}}{\mathrm{2}}\right) \\ $$$${T}_{\mathrm{1}} ×\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}=\mathrm{2}{cos}\left({a}+{b}\right)×{sin}\frac{{b}}{\mathrm{2}}={sin}\left({a}+\frac{\mathrm{3}{b}}{\mathrm{2}}\right)−{sin}\left({a}+\frac{{b}}{\mathrm{2}}\right) \\ $$$${T}_{\mathrm{2}} ×\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}=\mathrm{2}{cos}\left({a}+\mathrm{2}{b}\right)×{sin}\frac{{b}}{\mathrm{2}}={sin}\left({a}+\frac{\mathrm{5}{b}}{\mathrm{2}}\right)−{sin}\left({a}+\frac{\mathrm{3}{b}}{\mathrm{2}}\right) \\ $$$$… \\ $$$$…. \\ $$$${T}_{{n}} ×\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}=\mathrm{2}{cos}\left({a}+{nb}\right)×{sin}\frac{{b}}{\mathrm{2}}={sin}\left({a}+\frac{\left(\mathrm{2}{n}+\mathrm{1}\right){b}}{\mathrm{2}}\right)−{sin}\left({a}+\frac{\left(\mathrm{2}{n}−\mathrm{1}\right){b}}{\mathrm{2}}\right) \\ $$$${add}\:{LHS}\:{and}\:{RHS} \\ $$$${S}×\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}={sin}\left({a}+\frac{\left(\mathrm{2}{n}+\mathrm{1}\right){b}}{\mathrm{2}}\right)−{sin}\left({a}−\frac{{b}}{\mathrm{2}}\right) \\ $$$${so}\:{S}=\frac{{sin}\left({a}+\frac{\left(\mathrm{2}{n}+\mathrm{1}\right){b}}{\mathrm{2}}\right)−{sin}\left({a}−\frac{{b}}{\mathrm{2}}\right)}{\mathrm{2}{sin}\frac{{b}}{\mathrm{2}}} \\ $$
Commented by TawaTawa last updated on 29/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by mind is power last updated on 29/Oct/19
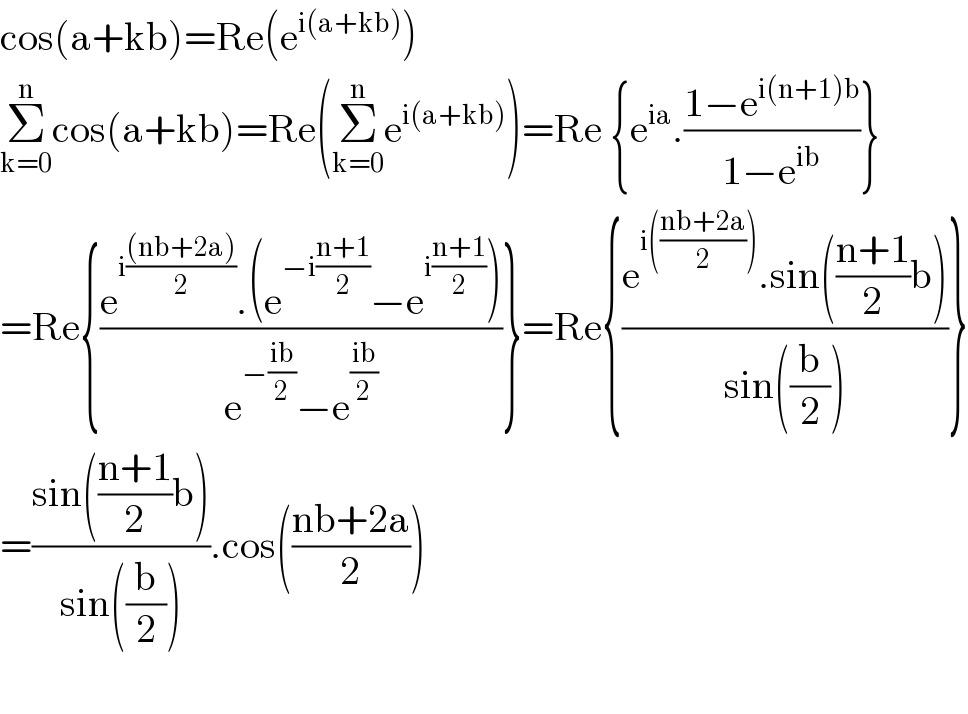
$$\mathrm{cos}\left(\mathrm{a}+\mathrm{kb}\right)=\mathrm{Re}\left(\mathrm{e}^{\mathrm{i}\left(\mathrm{a}+\mathrm{kb}\right)} \right) \\ $$$$\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{cos}\left(\mathrm{a}+\mathrm{kb}\right)=\mathrm{Re}\left(\underset{\mathrm{k}=\mathrm{0}} {\overset{\mathrm{n}} {\sum}}\mathrm{e}^{\mathrm{i}\left(\mathrm{a}+\mathrm{kb}\right)} \right)=\mathrm{Re}\:\left\{\mathrm{e}^{\mathrm{ia}} .\frac{\mathrm{1}−\mathrm{e}^{\mathrm{i}\left(\mathrm{n}+\mathrm{1}\right)\mathrm{b}} }{\mathrm{1}−\mathrm{e}^{\mathrm{ib}} }\right\} \\ $$$$=\mathrm{Re}\left\{\frac{\mathrm{e}^{\mathrm{i}\frac{\left(\mathrm{nb}+\mathrm{2a}\right)}{\mathrm{2}}} .\left(\mathrm{e}^{−\mathrm{i}\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}} −\mathrm{e}^{\mathrm{i}\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}} \right)}{\mathrm{e}^{−\frac{\mathrm{ib}}{\mathrm{2}}} −\mathrm{e}^{\frac{\mathrm{ib}}{\mathrm{2}}} }\right\}=\mathrm{Re}\left\{\frac{\mathrm{e}^{\mathrm{i}\left(\frac{\mathrm{nb}+\mathrm{2a}}{\mathrm{2}}\right)} .\mathrm{sin}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\mathrm{b}\right)}{\mathrm{sin}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)}\right\} \\ $$$$=\frac{\mathrm{sin}\left(\frac{\mathrm{n}+\mathrm{1}}{\mathrm{2}}\mathrm{b}\right)}{\mathrm{sin}\left(\frac{\mathrm{b}}{\mathrm{2}}\right)}.\mathrm{cos}\left(\frac{\mathrm{nb}+\mathrm{2a}}{\mathrm{2}}\right) \\ $$$$ \\ $$
Commented by TawaTawa last updated on 29/Oct/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
