Question Number 134215 by Abdoulaye last updated on 01/Mar/21
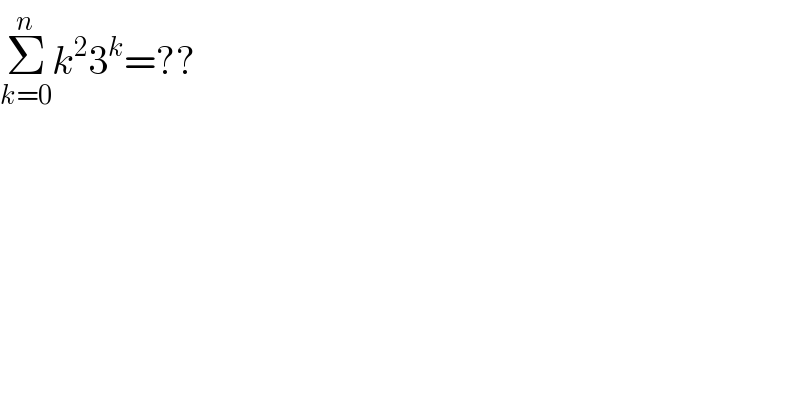
$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \mathrm{3}^{{k}} =?? \\ $$
Answered by mr W last updated on 01/Mar/21
![generally: S=Σ_(k=0) ^n k^2 p^k pS=Σ_(k=0) ^n (k+1−1)^2 p^(k+1) pS=Σ_(k=0) ^n [(k+1)^2 −2k−1]p^(k+1) pS=Σ_(k=0) ^n (k+1)^2 p^(k+1) −2Σ_(k=0) ^n kp^(k+1) −Σ_(k=0) ^n p^(k+1) pS=(n+1)^2 p^(n+1) +S−2pΣ_(k=0) ^n kp^k −Σ_(k=0) ^n p^(k+1) (p−1)S=(n+1)^2 p^(n+1) −2pΣ_(k=0) ^n kp^k −((p(p^(n+1) −1))/(p−1)) ⇒S=(1/(p−1))(n+1)^2 p^(n+1) −((2p)/(p−1))Σ_(k=0) ^n kp^k −((p(p^(n+1) −1))/((p−1)^2 )) with Σ_(k=0) ^n kp^k you have already got.](https://www.tinkutara.com/question/Q134225.png)
$${generally}: \\ $$$${S}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} {p}^{{k}} \\ $$$${pS}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}−\mathrm{1}\right)^{\mathrm{2}} {p}^{{k}+\mathrm{1}} \\ $$$${pS}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left[\left({k}+\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}{k}−\mathrm{1}\right]{p}^{{k}+\mathrm{1}} \\ $$$${pS}=\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left({k}+\mathrm{1}\right)^{\mathrm{2}} {p}^{{k}+\mathrm{1}} −\mathrm{2}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{kp}^{{k}+\mathrm{1}} −\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{p}^{{k}+\mathrm{1}} \\ $$$${pS}=\left({n}+\mathrm{1}\right)^{\mathrm{2}} {p}^{{n}+\mathrm{1}} +{S}−\mathrm{2}{p}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{kp}^{{k}} −\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{p}^{{k}+\mathrm{1}} \\ $$$$\left({p}−\mathrm{1}\right){S}=\left({n}+\mathrm{1}\right)^{\mathrm{2}} {p}^{{n}+\mathrm{1}} −\mathrm{2}{p}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{kp}^{{k}} −\frac{{p}\left({p}^{{n}+\mathrm{1}} −\mathrm{1}\right)}{{p}−\mathrm{1}} \\ $$$$\Rightarrow{S}=\frac{\mathrm{1}}{{p}−\mathrm{1}}\left({n}+\mathrm{1}\right)^{\mathrm{2}} {p}^{{n}+\mathrm{1}} −\frac{\mathrm{2}{p}}{{p}−\mathrm{1}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{kp}^{{k}} −\frac{{p}\left({p}^{{n}+\mathrm{1}} −\mathrm{1}\right)}{\left({p}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${with}\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{kp}^{{k}} \:{you}\:{have}\:{already}\:{got}. \\ $$
Commented by mr W last updated on 01/Mar/21

$${this}\:{is}\:{a}\:{general}\:{way},\:{you}\:{should}\:{be} \\ $$$${able}\:{to}\:{get} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{3}} \mathrm{4}^{{k}} =??? \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{4}} \mathrm{5}^{{k}} =???? \\ $$$${etc}. \\ $$
Answered by mindispower last updated on 01/Mar/21
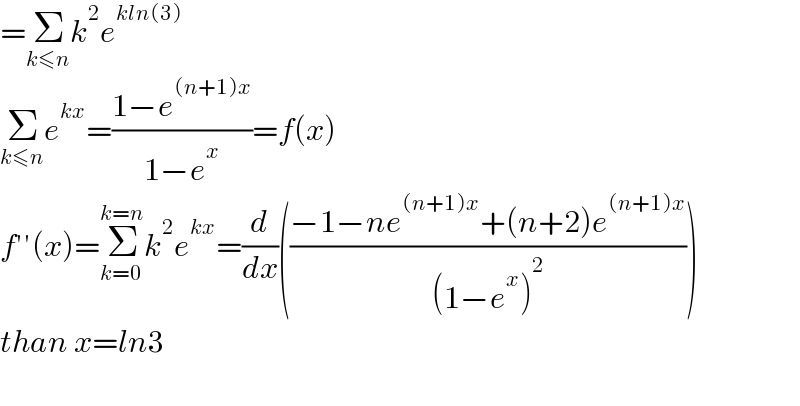
$$=\underset{{k}\leqslant{n}} {\sum}{k}^{\mathrm{2}} {e}^{{kln}\left(\mathrm{3}\right)} \\ $$$$\underset{{k}\leqslant{n}} {\sum}{e}^{{kx}} =\frac{\mathrm{1}−{e}^{\left({n}+\mathrm{1}\right){x}} }{\mathrm{1}−{e}^{{x}} }={f}\left({x}\right) \\ $$$${f}''\left({x}\right)=\underset{{k}=\mathrm{0}} {\overset{{k}={n}} {\sum}}{k}^{\mathrm{2}} {e}^{{kx}} =\frac{{d}}{{dx}}\left(\frac{−\mathrm{1}−{ne}^{\left({n}+\mathrm{1}\right){x}} +\left({n}+\mathrm{2}\right){e}^{\left({n}+\mathrm{1}\right){x}} }{\left(\mathrm{1}−{e}^{{x}} \right)^{\mathrm{2}} }\right) \\ $$$${than}\:{x}={ln}\mathrm{3} \\ $$$$ \\ $$
Commented by Abdoulaye last updated on 01/Mar/21
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
Answered by Ñï= last updated on 01/Mar/21
![Σ_(k=0) ^n k^2 3^k =[(xD)^2 Σ_(k=0) ^n x^k ]_(x=3) =[(xD)^2 ((x^(n+1) −1)/(x−1))]_(x=3) =[xD((nx^(n+2) −(n+1)x^(n+1) +x)/((x−1)^2 ))]_(x=3) xD=x(d/dx) ........](https://www.tinkutara.com/question/Q134248.png)
$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{k}^{\mathrm{2}} \mathrm{3}^{{k}} \\ $$$$=\left[\left({xD}\right)^{\mathrm{2}} \underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{x}^{{k}} \right]_{{x}=\mathrm{3}} \\ $$$$=\left[\left({xD}\right)^{\mathrm{2}} \frac{{x}^{{n}+\mathrm{1}} −\mathrm{1}}{{x}−\mathrm{1}}\right]_{{x}=\mathrm{3}} \\ $$$$=\left[{xD}\frac{{nx}^{{n}+\mathrm{2}} −\left({n}+\mathrm{1}\right){x}^{{n}+\mathrm{1}} +{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\right]_{{x}=\mathrm{3}} \\ $$$${xD}={x}\frac{{d}}{{dx}} \\ $$$$…….. \\ $$
