Question Number 139257 by bobhans last updated on 25/Apr/21
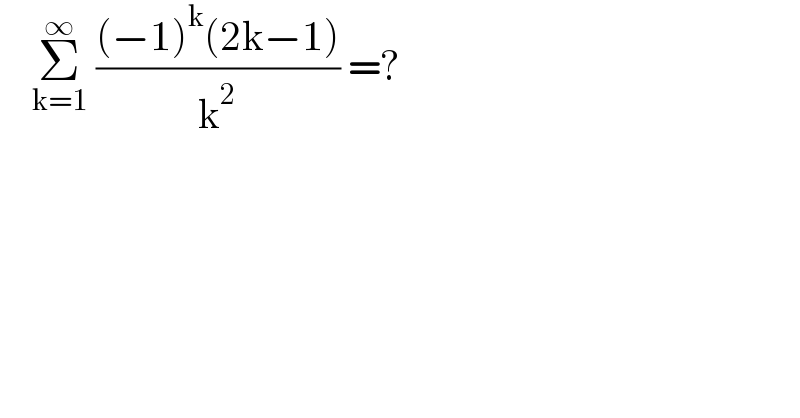
$$\:\:\:\:\underset{\mathrm{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left(−\mathrm{1}\right)^{\mathrm{k}} \left(\mathrm{2k}−\mathrm{1}\right)}{\mathrm{k}^{\mathrm{2}} }\:=? \\ $$
Answered by john_santu last updated on 25/Apr/21
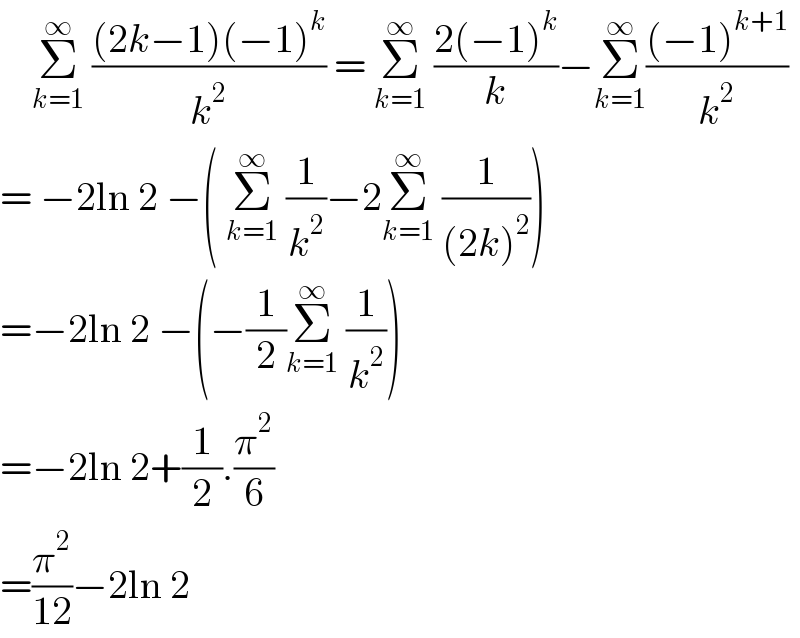
$$\:\:\:\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\left(\mathrm{2}{k}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{{k}} }{{k}^{\mathrm{2}} }\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{2}\left(−\mathrm{1}\right)^{{k}} }{{k}}−\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}^{\mathrm{2}} } \\ $$$$=\:−\mathrm{2ln}\:\mathrm{2}\:−\left(\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }−\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\left(\mathrm{2}{k}\right)^{\mathrm{2}} }\right) \\ $$$$=−\mathrm{2ln}\:\mathrm{2}\:−\left(−\frac{\mathrm{1}}{\mathrm{2}}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} }\right) \\ $$$$=−\mathrm{2ln}\:\mathrm{2}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{12}}−\mathrm{2ln}\:\mathrm{2}\: \\ $$
Answered by mathmax by abdo last updated on 25/Apr/21
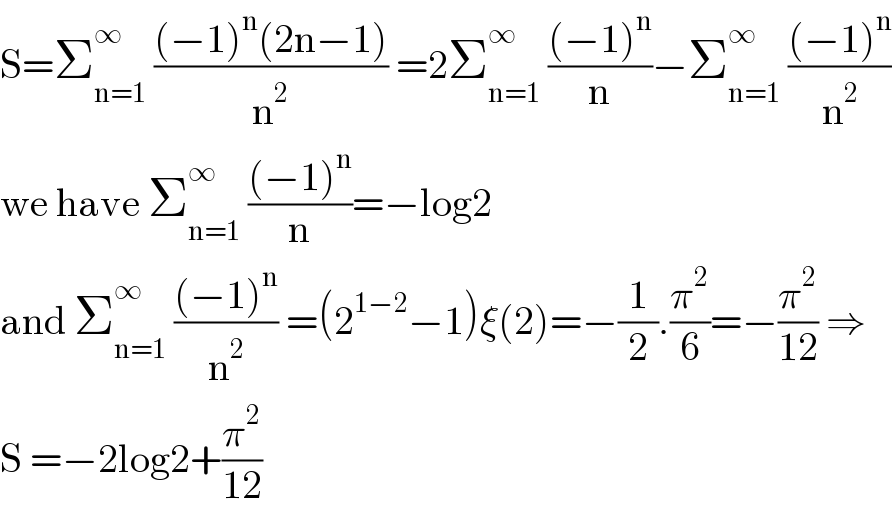
$$\mathrm{S}=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \left(\mathrm{2n}−\mathrm{1}\right)}{\mathrm{n}^{\mathrm{2}} }\:=\mathrm{2}\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$\mathrm{we}\:\mathrm{have}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}}=−\mathrm{log2} \\ $$$$\mathrm{and}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:=\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)=−\frac{\mathrm{1}}{\mathrm{2}}.\frac{\pi^{\mathrm{2}} }{\mathrm{6}}=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:\Rightarrow \\ $$$$\mathrm{S}\:=−\mathrm{2log2}+\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
