Question Number 137523 by SOMEDAVONG last updated on 03/Apr/21

$$\mathrm{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{x}!−\mathrm{1}}{\mathrm{x}} \\ $$
Answered by Dwaipayan Shikari last updated on 03/Apr/21
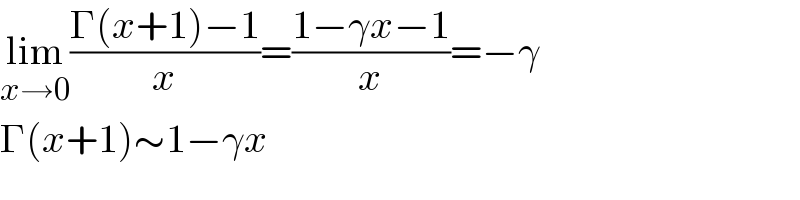
$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\Gamma\left({x}+\mathrm{1}\right)−\mathrm{1}}{{x}}=\frac{\mathrm{1}−\gamma{x}−\mathrm{1}}{{x}}=−\gamma \\ $$$$\Gamma\left({x}+\mathrm{1}\right)\sim\mathrm{1}−\gamma{x} \\ $$
