Question Number 5821 by FilupSmith last updated on 30/May/16

$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{x}^{{x}} \\ $$
Answered by bahmanfeshki last updated on 27/Feb/17
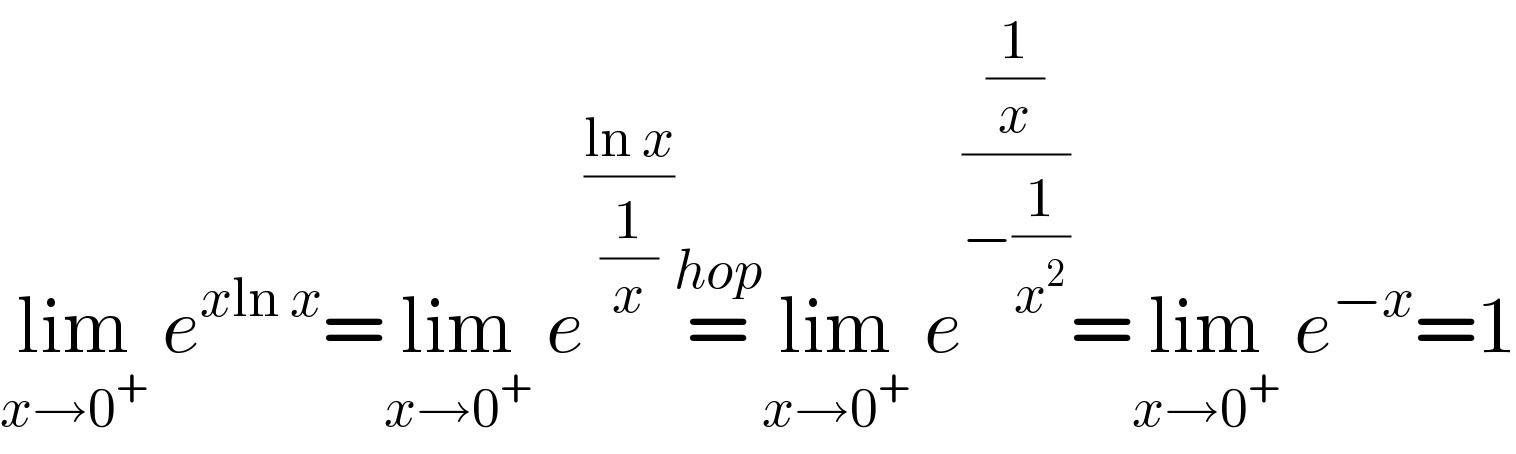
$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{e}^{{x}\mathrm{ln}\:{x}} =\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{e}^{\frac{\mathrm{ln}\:{x}}{\frac{\mathrm{1}}{{x}}}} \overset{{hop}} {=}\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{e}^{\frac{\frac{\mathrm{1}}{{x}}}{−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}} =\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{e}^{−{x}} =\mathrm{1} \\ $$
