Question Number 70360 by Hassen_Timol last updated on 03/Oct/19
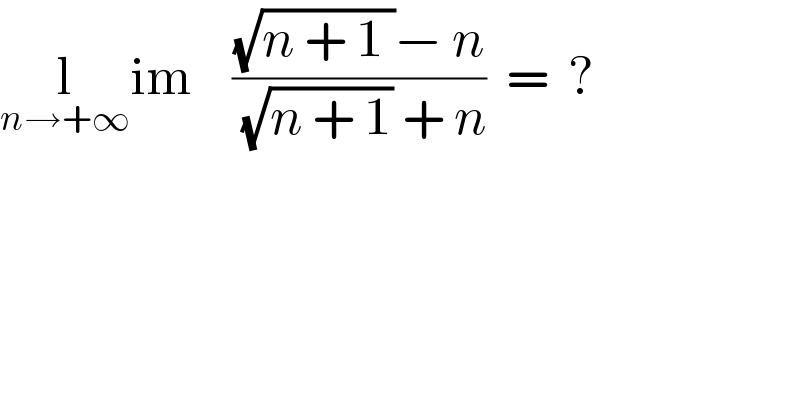
$$\underset{{n}\rightarrow+\infty} {\mathrm{l}im}\:\:\:\:\frac{\sqrt{{n}\:+\:\mathrm{1}\:}−\:{n}}{\:\sqrt{{n}\:+\:\mathrm{1}}\:+\:{n}}\:\:=\:\:? \\ $$
Answered by mind is power last updated on 03/Oct/19
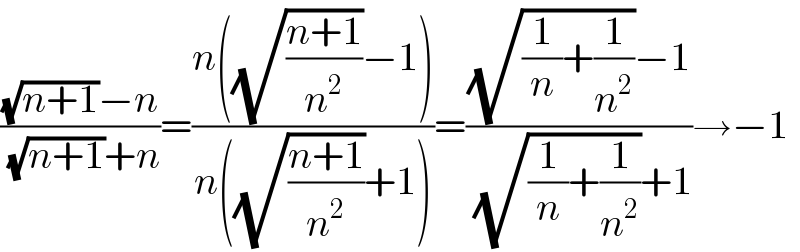
$$\frac{\sqrt{{n}+\mathrm{1}}−{n}}{\:\sqrt{{n}+\mathrm{1}}+{n}}=\frac{{n}\left(\sqrt{\frac{{n}+\mathrm{1}}{{n}^{\mathrm{2}} }}−\mathrm{1}\right)}{{n}\left(\sqrt{\frac{{n}+\mathrm{1}}{{n}^{\mathrm{2}} }}+\mathrm{1}\right)}=\frac{\sqrt{\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}−\mathrm{1}}{\:\sqrt{\frac{\mathrm{1}}{{n}}+\frac{\mathrm{1}}{{n}^{\mathrm{2}} }}+\mathrm{1}}\rightarrow−\mathrm{1} \\ $$
Commented by Hassen_Timol last updated on 03/Oct/19

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sooo}\:\mathrm{much}\:!!! \\ $$
