Question Number 5629 by LMTV last updated on 23/May/16
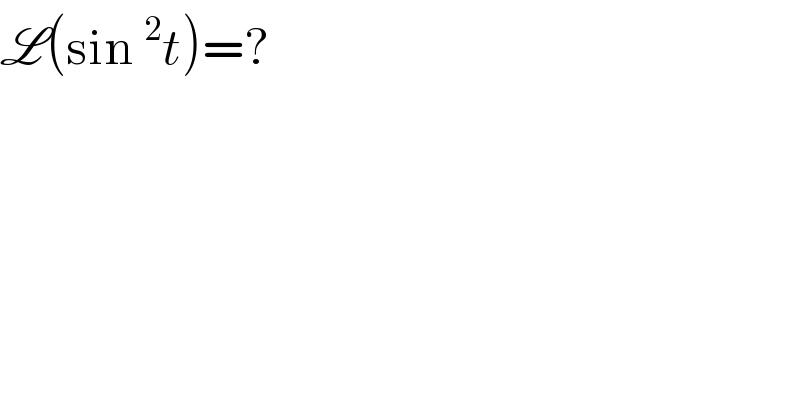
$$\mathscr{L}\left(\mathrm{sin}\:^{\mathrm{2}} {t}\right)=? \\ $$
Commented by FilupSmith last updated on 23/May/16
$$\mathrm{Laplace}\:\mathrm{transform}? \\ $$
Commented by LMTV last updated on 23/May/16

$${yes}\:>\smallsmile< \\ $$
Commented by FilupSmith last updated on 23/May/16
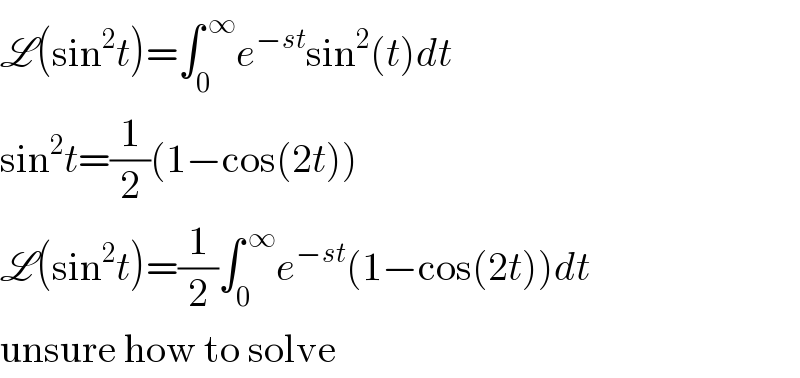
$$\mathscr{L}\left(\mathrm{sin}^{\mathrm{2}} {t}\right)=\int_{\mathrm{0}} ^{\:\infty} {e}^{−{st}} \mathrm{sin}^{\mathrm{2}} \left({t}\right){dt} \\ $$$$\mathrm{sin}^{\mathrm{2}} {t}=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2}{t}\right)\right) \\ $$$$\mathscr{L}\left(\mathrm{sin}^{\mathrm{2}} {t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\infty} {e}^{−{st}} \left(\mathrm{1}−\mathrm{cos}\left(\mathrm{2}{t}\right)\right){dt} \\ $$$$\mathrm{unsure}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve} \\ $$
Commented by Yozzii last updated on 23/May/16

$${e}^{\left({a}+{bi}\right){x}} ={e}^{{ax}} {e}^{{bix}} ={e}^{{ax}} \left({cosbx}+{isinbx}\right) \\ $$$$\Rightarrow{Re}\int{e}^{\left({a}+{bi}\right){x}} {dx}=\int{e}^{{ax}} {cosbxdx} \\ $$$$\therefore\int{e}^{{ax}} {cosbxdx}={Re}\left(\frac{\mathrm{1}}{{a}+{bi}}{e}^{\left({a}+{bi}\right){x}} \right)+{C} \\ $$$$\int{e}^{{ax}} {cosbxdx}={Re}\left(\frac{\left({a}−{bi}\right){e}^{\left({a}+{bi}\right){x}} }{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)+{C} \\ $$$$\int{e}^{{ax}} {cosbxdx}=\frac{{e}^{{ax}} \left({acosbx}+{bsinbx}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }+{C} \\ $$$${Let}\:{a}=−{s}\:{and}\:{b}=\mathrm{2}. \\ $$$$\therefore\int{e}^{−{sx}} {cos}\mathrm{2}{xdx}=\frac{{e}^{−{sx}} \left(\mathrm{2}{sin}\mathrm{2}{x}−{scos}\mathrm{2}{x}\right)}{{s}^{\mathrm{2}} +\mathrm{4}}+{C} \\ $$$$\therefore\mathscr{L}\left({sin}^{\mathrm{2}} {t}\right)=\frac{\mathrm{1}}{\mathrm{2}}\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left(\frac{−{e}^{−{st}} }{{s}}+\frac{{e}^{−{st}} \left({scos}\mathrm{2}{t}−\mathrm{2}{sin}\mathrm{2}{t}\right)}{{s}^{\mathrm{2}} +\mathrm{4}}\right)\mid_{\mathrm{0}} ^{{m}} \\ $$$$\mathscr{L}\left({sin}^{\mathrm{2}} {t}\right)=\mathrm{0}.\mathrm{5}\underset{{m}\rightarrow\infty} {\mathrm{lim}}\left({e}^{−{sm}} \left(\frac{{scos}\mathrm{2}{m}−\mathrm{2}{sin}\mathrm{2}{m}}{{s}^{\mathrm{2}} +\mathrm{4}}−\frac{\mathrm{1}}{{s}}\right)+\frac{\mathrm{1}}{{s}}−\frac{{s}}{{s}^{\mathrm{2}} +\mathrm{4}}\right) \\ $$$$\mathscr{L}\left({sin}^{\mathrm{2}} {t}\right)=\mathrm{0}.\mathrm{5}\left(\frac{{s}^{\mathrm{2}} +\mathrm{4}−{s}^{\mathrm{2}} }{{s}\left({s}^{\mathrm{2}} +\mathrm{4}\right)}\right) \\ $$$$\mathscr{L}\left({sin}^{\mathrm{2}} {t}\right)=\frac{\mathrm{2}}{{s}\left({s}^{\mathrm{2}} +\mathrm{4}\right)} \\ $$
