Question Number 77856 by walidMTS last updated on 11/Jan/20
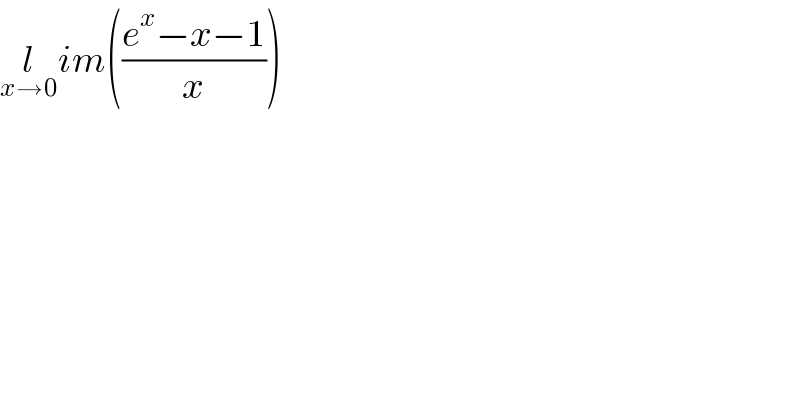
$$\underset{{x}\rightarrow\mathrm{0}} {{l}im}\left(\frac{{e}^{{x}} −{x}−\mathrm{1}}{{x}}\right) \\ $$
Commented by mathmax by abdo last updated on 11/Jan/20
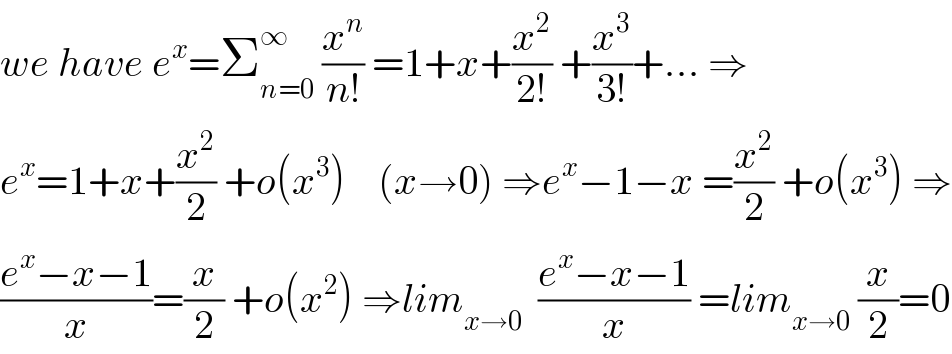
$${we}\:{have}\:{e}^{{x}} =\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}} }{{n}!}\:=\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}\:+\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+…\:\Rightarrow \\ $$$${e}^{{x}} =\mathrm{1}+{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({x}^{\mathrm{3}} \right)\:\:\:\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow{e}^{{x}} −\mathrm{1}−{x}\:=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({x}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$$\frac{{e}^{{x}} −{x}−\mathrm{1}}{{x}}=\frac{{x}}{\mathrm{2}}\:+{o}\left({x}^{\mathrm{2}} \right)\:\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\frac{{e}^{{x}} −{x}−\mathrm{1}}{{x}}\:={lim}_{{x}\rightarrow\mathrm{0}} \:\frac{{x}}{\mathrm{2}}=\mathrm{0} \\ $$
Answered by Rio Michael last updated on 11/Jan/20
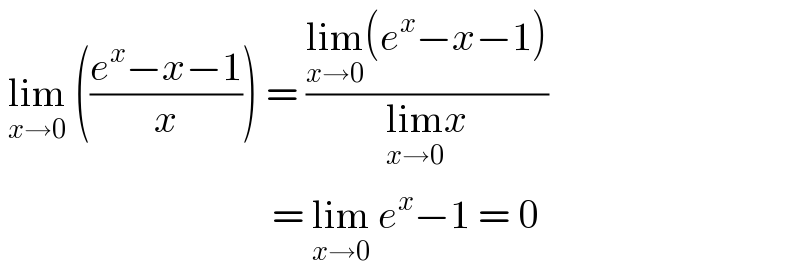
$$\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\left(\frac{{e}^{{x}} −{x}−\mathrm{1}}{{x}}\right)\:=\:\frac{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left({e}^{{x}} −{x}−\mathrm{1}\right)}{\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{x}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:{e}^{{x}} −\mathrm{1}\:=\:\mathrm{0} \\ $$
