Menu Close

l-x-0-im-x-sin-x-x-2-e-x-1-

Tinku Tara 0 Comments
Pin




Question Number 6703 by love math last updated on 15/Jul/16
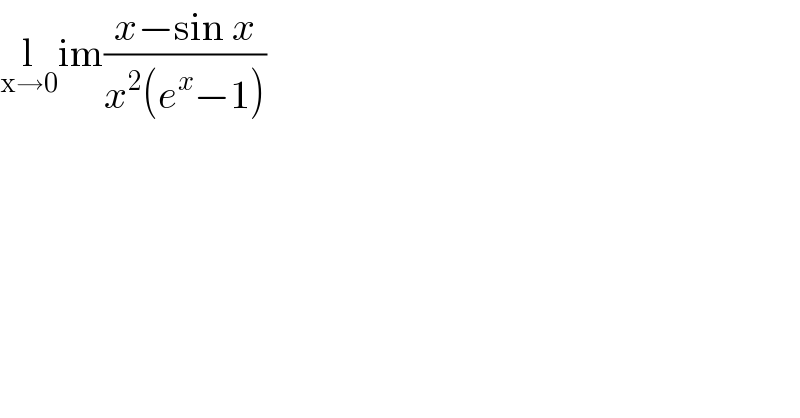
l_(x→0) im((x−sin x)/(x^2 (e^x −1)))
$$\underset{\mathrm{x}\rightarrow\mathrm{0}} {\mathrm{l}im}\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} \left({e}^{{x}} −\mathrm{1}\right)} \\ $$
Answered by FilupSmith last updated on 15/Jul/16
L=lim_(x→0) ((x−sin x)/(x^2 e^x −x^2 ))=((0−0)/(0−0))=(0/0) use L′Hopital′s law ∴L=lim_(x→0) ((1−cos x)/(2xe^x +x^2 e^x −2x))=((1−1)/(0+0−0))=(0/0) apply law again ∴L=lim_(x→0) ((sin x)/(2e^x (x+1)+2xe^x +x^2 e^x −2))=(0/(2+0+0−2)) apply law again ∴L=lim_(x→0) ((cos x)/(2e^x (x+2)+2e^x (x+1)+2xe^x +x^2 e^x )) L=(1/(2(2)+2(1)+0+0)) ∴L=(1/6) ∴ lim_(x→0) ((x−sin x)/(x^2 (e^x −1))) = (1/6)
$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} {e}^{{x}} −{x}^{\mathrm{2}} }=\frac{\mathrm{0}−\mathrm{0}}{\mathrm{0}−\mathrm{0}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\mathrm{use}\:{L}'\mathrm{Hopital}'\mathrm{s}\:\mathrm{law} \\ $$$$\therefore{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{cos}\:{x}}{\mathrm{2}{xe}^{{x}} +{x}^{\mathrm{2}} {e}^{{x}} −\mathrm{2}{x}}=\frac{\mathrm{1}−\mathrm{1}}{\mathrm{0}+\mathrm{0}−\mathrm{0}}=\frac{\mathrm{0}}{\mathrm{0}} \\ $$$$\mathrm{apply}\:\mathrm{law}\:\mathrm{again} \\ $$$$\therefore{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{sin}\:{x}}{\mathrm{2}{e}^{{x}} \left({x}+\mathrm{1}\right)+\mathrm{2}{xe}^{{x}} +{x}^{\mathrm{2}} {e}^{{x}} −\mathrm{2}}=\frac{\mathrm{0}}{\mathrm{2}+\mathrm{0}+\mathrm{0}−\mathrm{2}} \\ $$$$\mathrm{apply}\:\mathrm{law}\:\mathrm{again} \\ $$$$\therefore{L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}}{\mathrm{2}{e}^{{x}} \left({x}+\mathrm{2}\right)+\mathrm{2}{e}^{{x}} \left({x}+\mathrm{1}\right)+\mathrm{2}{xe}^{{x}} +{x}^{\mathrm{2}} {e}^{{x}} } \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}\right)+\mathrm{2}\left(\mathrm{1}\right)+\mathrm{0}+\mathrm{0}} \\ $$$$\therefore{L}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$$$\therefore\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}−\mathrm{sin}\:{x}}{{x}^{\mathrm{2}} \left({e}^{{x}} −\mathrm{1}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{6}} \\ $$
Answered by sou1618 last updated on 15/Jul/16
=lim_(x→0) ((x−sinx)/(x^2 (e^x −1))) (∵lim_(x→0) ((e^x −1)/x)=1) =lim_(x→0) ((x−sinx)/x^3 ) L=lim_(x→0) ((x−sinx)/x^3 ) x=3t =lim_(t→0) ((3t−sin3t)/(27t^3 )) (∵sin(3t)=3sint−4sin^3 t) =lim_(t→0) ((3t−3sint+4sin^3 t)/(27t^3 )) =lim_(t→0) ((3t−3sint)/(27t^3 ))+(4/(27)) =(1/9)(lim_(t→0) ((t−sint)/t^3 ))+(4/(27)) =(1/9)L+(4/(27)) L=(1/9)L+(4/(27)) (8/9)L=(4/(27)) L=(1/6) ∴lim_(x→0) ((x−sinx)/(x^2 (e^x −1)))=(1/6)
$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−{sinx}}{{x}^{\mathrm{2}} \left({e}^{{x}} −\mathrm{1}\right)} \\ $$$$\:\:\:\left(\because\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{e}^{{x}} −\mathrm{1}}{{x}}=\mathrm{1}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−{sinx}}{{x}^{\mathrm{3}} } \\ $$$$ \\ $$$${L}=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−{sinx}}{{x}^{\mathrm{3}} } \\ $$$${x}=\mathrm{3}{t} \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{t}−{sin}\mathrm{3}{t}}{\mathrm{27}{t}^{\mathrm{3}} } \\ $$$$\:\left(\because{sin}\left(\mathrm{3}{t}\right)=\mathrm{3}{sint}−\mathrm{4}{sin}^{\mathrm{3}} {t}\right) \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{t}−\mathrm{3}{sint}+\mathrm{4}{sin}^{\mathrm{3}} {t}}{\mathrm{27}{t}^{\mathrm{3}} } \\ $$$$=\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{3}{t}−\mathrm{3}{sint}}{\mathrm{27}{t}^{\mathrm{3}} }+\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{t}−{sint}}{{t}^{\mathrm{3}} }\right)+\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}{L}+\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$ \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{9}}{L}+\frac{\mathrm{4}}{\mathrm{27}} \\ $$$$\frac{\mathrm{8}}{\mathrm{9}}{L}=\frac{\mathrm{4}}{\mathrm{27}} \\ $$$${L}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$$$ \\ $$$$\therefore\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{{x}−{sinx}}{{x}^{\mathrm{2}} \left({e}^{{x}} −\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{6}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *