Menu Close

let-A-1-1-3-1-1-calculate-A-n-2-find-e-A-and-e-A-3-find-cosA-and-sinA-

Tinku Tara 0 Comments
Pin




Question Number 75735 by mathmax by abdo last updated on 16/Dec/19
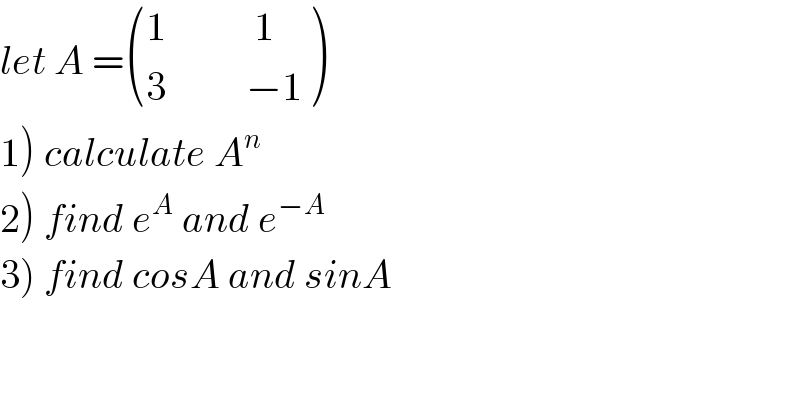
let A = (((1 1)),((3 −1)) ) 1) calculate A^n 2) find e^A and e^(−A) 3) find cosA and sinA
$${let}\:{A}\:=\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:−\mathrm{1}}\end{pmatrix} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{A}^{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{e}^{{A}} \:{and}\:{e}^{−{A}} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{cosA}\:{and}\:{sinA} \\ $$
Commented by abdomathmax last updated on 22/Dec/19
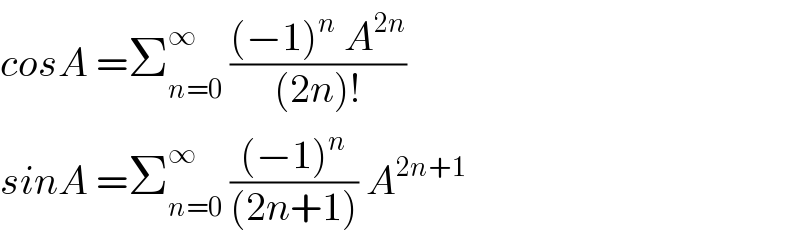
cosA =Σ_(n=0) ^∞ (((−1)^n A^(2n) )/((2n)!)) sinA =Σ_(n=0) ^∞ (((−1)^n )/((2n+1))) A^(2n+1)
$${cosA}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} \:{A}^{\mathrm{2}{n}} }{\left(\mathrm{2}{n}\right)!} \\ $$$${sinA}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)}\:{A}^{\mathrm{2}{n}+\mathrm{1}} \\ $$
Commented by mathmax by abdo last updated on 22/Dec/19
Pc(x) =det(A−xI) = determinant (((1−x 1)),((3 −1−x)))=−(1+x)(1−x)−3 =x^2 −1−3 =x^2 −4 the proper values are λ_1 =2 and λ_2 =−2 we hsve x^n =P_c (x)Q(x) +u_n x +v_(n ) ⇒ 2^n =2u_n +v_n and (−2)^n =−2u_n +v_n ⇒ { ((2u_n +v_n =2^n )),((−2u_n +v_n =(−2)^n ⇒4u_n =2^n −(−2)^n ⇒ u_n =((2^n −(−2)^n )/4))) :} v_n =2^n −2u_n =2^n −((2^n −(−2)^n )/2)=((2.2^n −2^n +(−2)^n )/2) =((2^n +(−2)^n )/2) also we have A^n = u_n A +v_n I =((2^n −(−2)^n )/4) (((1 1)),((3 −1)) ) +((2^n +(−2)^n )/2) (((1 0)),((0 1)) ) = (((((2^n −(−2)^n )/4) ((2^n −(−2)^n )/4))),(((3/4)( 2^n −(−2)^n ) −((2^n −(−2)^n )/4))) ) + (((((2^n +(−2)^n )/2) 0)),((0 ((2^n +(−2)^n )/2))) ) = ((( ((2^n −(−2)^n +2.2^n +2.(−2)^n )/4) ((2^n −(−2)^n )/4))),(((3/4)(2^n −(−2)^n ) ((−2^n +(−2)^n +2.2^n +2.(−2)^n )/4))) )
$${Pc}\left({x}\right)\:={det}\left({A}−{xI}\right)\:=\begin{vmatrix}{\mathrm{1}−{x}\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}−{x}}\end{vmatrix}=−\left(\mathrm{1}+{x}\right)\left(\mathrm{1}−{x}\right)−\mathrm{3} \\ $$$$={x}^{\mathrm{2}} −\mathrm{1}−\mathrm{3}\:={x}^{\mathrm{2}} −\mathrm{4} \\ $$$${the}\:{proper}\:{values}\:{are}\:\:\lambda_{\mathrm{1}} =\mathrm{2}\:{and}\:\lambda_{\mathrm{2}} =−\mathrm{2} \\ $$$${we}\:{hsve}\:\:{x}^{{n}} \:={P}_{{c}} \left({x}\right){Q}\left({x}\right)\:+{u}_{{n}} {x}\:+{v}_{{n}\:} \:\:\Rightarrow\:\:\mathrm{2}^{{n}} \:=\mathrm{2}{u}_{{n}} +{v}_{{n}} \\ $$$${and}\:\:\left(−\mathrm{2}\right)^{{n}} \:=−\mathrm{2}{u}_{{n}} +{v}_{{n}} \:\Rightarrow \\ $$$$\begin{cases}{\mathrm{2}{u}_{{n}} \:+{v}_{{n}} =\mathrm{2}^{{n}} }\\{−\mathrm{2}{u}_{{n}} \:+{v}_{{n}} =\left(−\mathrm{2}\right)^{{n}} \:\:\Rightarrow\mathrm{4}{u}_{{n}} =\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} \:\Rightarrow\:{u}_{{n}} =\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\end{cases} \\ $$$${v}_{{n}} =\mathrm{2}^{{n}} −\mathrm{2}{u}_{{n}} =\mathrm{2}^{{n}} −\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} \:}{\mathrm{2}}=\frac{\mathrm{2}.\mathrm{2}^{{n}} −\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} }{\mathrm{2}}\:=\frac{\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} }{\mathrm{2}} \\ $$$${also}\:{we}\:{have}\:\:{A}^{{n}} \:=\:{u}_{{n}} \:{A}\:+{v}_{{n}} \:{I}\: \\ $$$$=\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\\{\mathrm{3}\:\:\:\:\:\:\:\:\:−\mathrm{1}}\end{pmatrix}\:\:+\frac{\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} }{\mathrm{2}}\:\begin{pmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\mathrm{1}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\\{\frac{\mathrm{3}}{\mathrm{4}}\left(\:\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} \right)\:\:\:\:\:\:\:\:−\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\end{pmatrix}\:\:+\:\begin{pmatrix}{\frac{\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} }{\mathrm{2}}\:\:\:\:\:\:\:\:\mathrm{0}}\\{\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} }{\mathrm{2}}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} \:+\mathrm{2}.\mathrm{2}^{{n}} \:+\mathrm{2}.\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\\{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} \right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{−\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} \:+\mathrm{2}.\mathrm{2}^{{n}} \:+\mathrm{2}.\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\end{pmatrix} \\ $$
Commented by mathmax by abdo last updated on 22/Dec/19
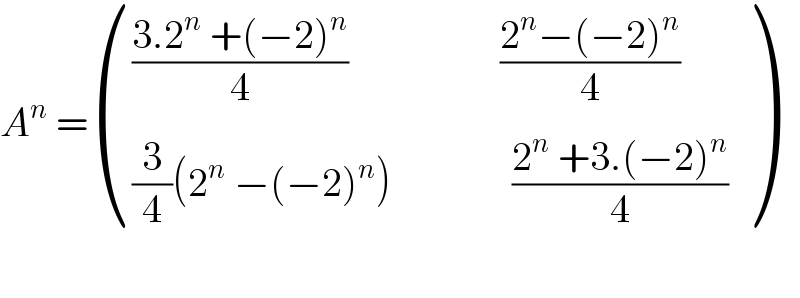
A^n = (((((3.2^n +(−2)^n )/4) ((2^n −(−2)^n )/4))),(((3/4)(2^n −(−2)^n ) ((2^n +3.(−2)^n )/4))) )
$${A}^{{n}} \:=\begin{pmatrix}{\frac{\mathrm{3}.\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\\{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{2}^{{n}} \:−\left(−\mathrm{2}\right)^{{n}} \right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} \:+\mathrm{3}.\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\end{pmatrix} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 22/Dec/19
e^A =Σ_(n=0) ^∞ (A^n /(n!)) =Σ_(n=0) ^∞ (1/(n!)) (((((3.2^n +(−2)^n )/4) ((2^n −(−2)^n )/4))),(((3/4)(2^n −(−2)^n ) ((2^n +3(−2)^n )/4))) ) = ((((3/4)Σ_(n=0) ^∞ (2^n /(n!)) +(1/4)Σ_(n=0) ^∞ (((−2)^n )/(n!)) (1/4) Σ_(n=0) ^∞ (2^n /(n!))−(1/4)Σ_(n=0) ^∞ (((−2)^n )/(n!)))),(((3/4)Σ_(n=0) ^∞ (2^n /(n!))−(3/4)Σ_(n=0) ^∞ (((−2)^n )/(n!)) (1/4)Σ_(n=0) ^∞ (2^n /(n!))+(3/4)Σ_(n=0) ^∞ (((−2)^n )/(n!)))) ) = ((((3/4)e^2 +(1/4)e^(−2) (1/4)e^2 −(1/4)e^(−2) )),(((3/4)e^2 −(3/4)e^(−2) (1/4)e^2 +(3/4)e^(−2) )) ) we use the same way to find e^(−A) =Σ_(n=0) ^∞ (((−A)^n )/(n!))
$${e}^{{A}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{A}^{{n}} }{{n}!}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}!}\begin{pmatrix}{\frac{\mathrm{3}.\mathrm{2}^{{n}} \:+\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\\{\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{2}^{{n}} −\left(−\mathrm{2}\right)^{{n}} \right)\:\:\:\:\:\:\:\frac{\mathrm{2}^{{n}} \:+\mathrm{3}\left(−\mathrm{2}\right)^{{n}} }{\mathrm{4}}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\frac{\mathrm{3}}{\mathrm{4}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{{n}} }{{n}!}\:+\frac{\mathrm{1}}{\mathrm{4}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{{n}} }{{n}!}\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\:\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{{n}} }{{n}!}−\frac{\mathrm{1}}{\mathrm{4}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{{n}} }{{n}!}}\\{\frac{\mathrm{3}}{\mathrm{4}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{{n}} }{{n}!}−\frac{\mathrm{3}}{\mathrm{4}}\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\left(−\mathrm{2}\right)^{{n}} }{{n}!}\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{2}^{{n}} }{{n}!}+\frac{\mathrm{3}}{\mathrm{4}}\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{2}\right)^{{n}} }{{n}!}}\end{pmatrix} \\ $$$$=\begin{pmatrix}{\frac{\mathrm{3}}{\mathrm{4}}{e}^{\mathrm{2}} \:+\frac{\mathrm{1}}{\mathrm{4}}{e}^{−\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{2}} \:−\frac{\mathrm{1}}{\mathrm{4}}{e}^{−\mathrm{2}} }\\{\frac{\mathrm{3}}{\mathrm{4}}{e}^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}{e}^{−\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}{e}^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}{e}^{−\mathrm{2}} }\end{pmatrix} \\ $$$${we}\:{use}\:{the}\:{same}\:{way}\:{to}\:{find}\:{e}^{−{A}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−{A}\right)^{{n}} }{{n}!} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *