Menu Close

Let-a-b-and-c-be-three-positive-real-numbers-Prove-that-a-b-c-a-2-bc-b-c-b-2-ca-c-a-c-2-ab-a-b-

Tinku Tara
Pin




Question Number 131465 by bramlexs22 last updated on 05/Feb/21
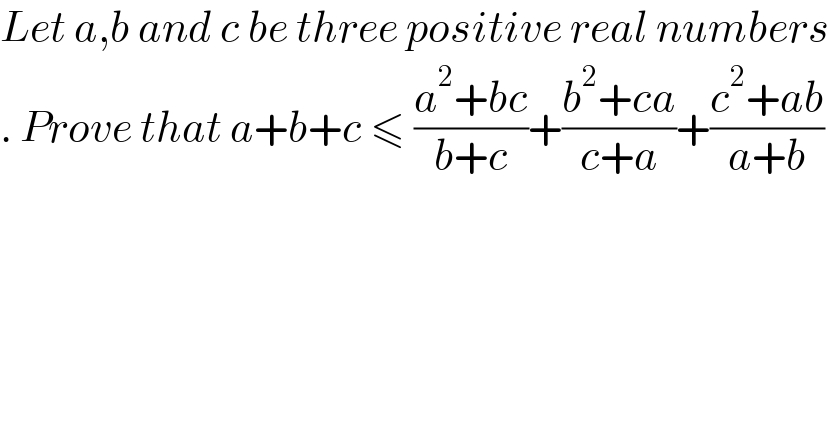
Let a,b and c be three positive real numbers . Prove that a+b+c ≤ ((a^2 +bc)/(b+c))+((b^2 +ca)/(c+a))+((c^2 +ab)/(a+b))
$${Let}\:{a},{b}\:{and}\:{c}\:{be}\:{three}\:{positive}\:{real}\:{numbers} \\ $$$$.\:{Prove}\:{that}\:{a}+{b}+{c}\:\leqslant\:\frac{{a}^{\mathrm{2}} +{bc}}{{b}+{c}}+\frac{{b}^{\mathrm{2}} +{ca}}{{c}+{a}}+\frac{{c}^{\mathrm{2}} +{ab}}{{a}+{b}} \\ $$
Answered by EDWIN88 last updated on 05/Feb/21
According to the identity ((a^2 +bc)/(b+c))−a=(((a−b)(a−c))/(b+c)) we can change our inequality into the form x(a−b)(a−c)+y(b−a)(b−c)+z(c−a)(c−b)≥0 in which x=(1/(b+c)) , y=(1/(c+a)) ,z=(1/(a+b)) WLOG ,assume a≥b≥c then x≤y≤z
$${According}\:{to}\:{the}\:{identity}\:\frac{{a}^{\mathrm{2}} +{bc}}{{b}+{c}}−{a}=\frac{\left({a}−{b}\right)\left({a}−{c}\right)}{{b}+{c}} \\ $$$${we}\:{can}\:{change}\:{our}\:{inequality}\:{into}\:{the}\:{form} \\ $$$${x}\left({a}−{b}\right)\left({a}−{c}\right)+{y}\left({b}−{a}\right)\left({b}−{c}\right)+{z}\left({c}−{a}\right)\left({c}−{b}\right)\geqslant\mathrm{0} \\ $$$${in}\:{which}\:{x}=\frac{\mathrm{1}}{{b}+{c}}\:,\:{y}=\frac{\mathrm{1}}{{c}+{a}}\:,{z}=\frac{\mathrm{1}}{{a}+{b}} \\ $$$${WLOG}\:,{assume}\:{a}\geqslant{b}\geqslant{c}\:{then}\:{x}\leqslant{y}\leqslant{z} \\ $$$$ \\ $$

Pin